题目内容
(本题满分12分)
已知数列 的前 n项和为
的前 n项和为 ,满足
,满足 ,且
,且 .
.
(Ⅰ)求 ,
, ;
;
(Ⅱ)若 ,求证:数列
,求证:数列 是等比数列。
是等比数列。
(Ⅲ)若 ,
求数列
,
求数列 的前n项和
的前n项和 。
。
【答案】
(1)  ,
, (2)证明数列是等比数列,主要是证明从第二项起每一项与前面 项的比值为定值,进而得到证明。
(2)证明数列是等比数列,主要是证明从第二项起每一项与前面 项的比值为定值,进而得到证明。
(3)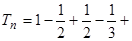 …
…
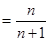
【解析】
试题分析:解(Ⅰ) ,
,
(Ⅱ)由 ①
①
得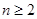 时,
时, ②
②
①-②得 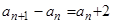
整理得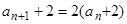
即 (
(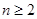 )
)
又∵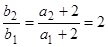
∴数列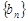 是以2为首项,2为公比的等比数列。
是以2为首项,2为公比的等比数列。
(Ⅲ)由(Ⅱ)得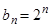
则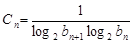
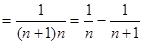
∴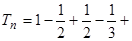 …
…
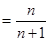
考点:数列的通项公式和求和的运用
点评:解决的关键是对于数列的概念的理解和运用,以及结合裂项法思想,将根据通项公式的特点来求和,得到结论,属于基础题。

练习册系列答案
相关题目
 <1,xÎR }.
<1,xÎR }. ,求实数a的取值范围.
,求实数a的取值范围. (
( ,
, 为常数),且方程
为常数),且方程 有两个实根为
有两个实根为 .
. 的解析式;
的解析式; 中,四边形
中,四边形 是边长为
是边长为 的正方形,
的正方形, ,
, 为
为 上的点,且
上的点,且 ⊥平面
⊥平面
 ⊥平面
⊥平面
 的大小;
的大小; 到平面
到平面