题目内容

a、b、c、d∈R，且a2＋b2＝c2＋d2＝1，则abcd的最小值等于

[　　]

A．

B．

C．－

D．－

答案：C
解析：


练习册系列答案
相关题目
设a、b、c、d∈R，若
a+bi
c+di
为实数，则（　　）
A、bc+ad≠0
B、bc-ad≠0
C、bc-ad=0
D、bc+ad=0
设a，b，c，d∈R，则条件甲：ac=2（b+d）是条件乙：方程x2+ax+b=0与方程x2+cx+d=0中至少有一个有实根的（　　）
A、充分而不必要条件B、必要而不充分条件C、充要条件D、既不充分也不必要条件
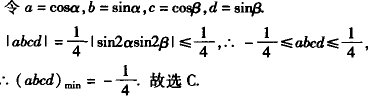
若函数f（x）=
bx+cx2+ax+1
（a，b，c∈R）（a，b，c，d∈R），其图象如图所示，则a+b+c=
4
4
．
设函数f（x）=ax3-2bx2+cx+4d（a、b、c、d∈R）图象C关于原点对称，且x=1时，f（x）取极小值-
23
．
（1）求f（x）的解析式；
（2）当x∈[-2，3]时，求函数f（x）的最大值．
命题：“已知a，b，c，d∈R，若a=b，c=d，则a+c=b+d”的逆否命题是：
已知a，b，c，d∈R，若a+c≠b+d，则a≠b或c≠d
已知a，b，c，d∈R，若a+c≠b+d，则a≠b或c≠d
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网