题目内容
若1+i是实系数方程x2+bx+c=0的一个根,则方程的另一个根为( )A..-1-i
B.-1+i
C.1-i
D.i
【答案】分析:把1+i代入实系数方程x2+bx+c=0,求出b,c,然后再求另一个根.
解答:解:依题意得(1+i)2+b(1+i)+c=(2+b)i+(b+c)=0,
∴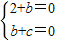 ,
,
∴b=-2,c=2,即方程x2-2x+2=0,
易得方程的另一个根为1-i.
故选C.
点评:本题考查复数的基本概念,一元二次方程的根的分布与系数的关系,考查计算能力,是基础题;也可以直接根据实系数方程,虚根成共轭复数,直接得到选项.
解答:解:依题意得(1+i)2+b(1+i)+c=(2+b)i+(b+c)=0,
∴
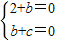 ,
,∴b=-2,c=2,即方程x2-2x+2=0,
易得方程的另一个根为1-i.
故选C.
点评:本题考查复数的基本概念,一元二次方程的根的分布与系数的关系,考查计算能力,是基础题;也可以直接根据实系数方程,虚根成共轭复数,直接得到选项.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
若1+i是实系数方程x2+bx+c=0的一个根,则方程的另一个根为( )
| A、.-1-i | B、-1+i | C、1-i | D、i |