题目内容
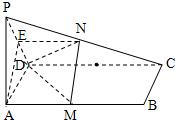如图，已知PA⊥矩形ABCD所在的平面，M、N分别是AB，PC的中点；若P-CD-A为45°的二面角，求证：平面MND⊥平面PDC；
分析：先由PA⊥矩形ABCD所在的平面?CD⊥面PAD?CD⊥PD?∠PDA是二面角P-CD-A的平面角?AE⊥面PCD．又由EN平行且等于AM?MN∥AE?MN⊥面PCD即可证得结论成立．
解答：解：仅仅观察平面MND和平面PDC，很难发现垂直的线索；
从二面角P-CD-A入手，易见CD⊥AD，CD⊥AP，
∴CD⊥面PAD，∴CD⊥PD，即∠PDA是二面角P-CD-A的平面角，
∴∠PDA=45°，那么在Rt△PAD中有AP=AD，
取PD中点E，则AE⊥PD，又由CD⊥面PAD得CD⊥AE，故AE⊥面PCD；
而EN平行且等于
DC，即EN平行且等于AM，
∴四边形AMNE是平行四边形，即MN∥AE；于是有MN⊥面PCD，
又∵MN在面MND内，
∴平面MND⊥平面PDC．
从二面角P-CD-A入手，易见CD⊥AD，CD⊥AP，
∴CD⊥面PAD，∴CD⊥PD，即∠PDA是二面角P-CD-A的平面角，
∴∠PDA=45°，那么在Rt△PAD中有AP=AD，
取PD中点E，则AE⊥PD，又由CD⊥面PAD得CD⊥AE，故AE⊥面PCD；
而EN平行且等于
| 1 |
| 2 |
∴四边形AMNE是平行四边形，即MN∥AE；于是有MN⊥面PCD，
又∵MN在面MND内，
∴平面MND⊥平面PDC．
点评：本题考查平面和平面垂直的判定和性质．在证明面面垂直时，其常用方法是在其中一个平面内找两条相交直线和另一平面内的某一条直线垂直
练习册系列答案
相关题目
如图，已知PA⊥矩形ABCD所在平面，M、N分别为AB、PC的中点；
如图，已知PA⊥矩形ABCD所在平面，M、N分别是AB、PC的中点．
