题目内容
用长度为定值l的铁丝围成一个底面边长是x,体积是V的正四棱柱形状的框架.(Ⅰ)试将V表示成x的函数,并指出x的取值范围;
(Ⅱ)当正四棱柱的底面边长和高之比是多少时,其体积最大?
【答案】分析:(Ⅰ)先用为定值l和底面边长x表示出正四棱柱的高,然后根据正四棱柱的体积公式等于底面积乘以高得到V与x的关系式,根据l-8x大于0得到x的范围;
(Ⅱ)求出V′,讨论导函数的正负决定函数的增减性得到函数的最大值时x的取值即可.
解答:解:(Ⅰ)由长度为定值l的铁丝围成的底面边长为x,则正四棱柱的高为 ,根据体积公式得:
,根据体积公式得:
V=x2• =
= x2-2x3,
x2-2x3,
又因为l-8x>0且x>0解得x的取值范围是(0, ).
).
(Ⅱ)求出V′= x-6x2=-6x(x-
x-6x2=-6x(x-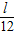 ),
),
在(0, )上,V′>0,函数单调递增;在(
)上,V′>0,函数单调递增;在(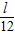 ,
, )上,V′<0,函数单调递减.
)上,V′<0,函数单调递减.
∴当x=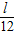 时,V取最大值.
时,V取最大值.
此时,正四棱柱的高为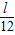 ,于是当正四棱柱底面边长和高之比是1时,其体积最大.
,于是当正四棱柱底面边长和高之比是1时,其体积最大.
点评:考查学生会根据实际问题选择合适的函数类型,掌握棱柱的体积公式,会利用导数求闭区间上函数的最值.
(Ⅱ)求出V′,讨论导函数的正负决定函数的增减性得到函数的最大值时x的取值即可.
解答:解:(Ⅰ)由长度为定值l的铁丝围成的底面边长为x,则正四棱柱的高为
 ,根据体积公式得:
,根据体积公式得:V=x2•
 =
= x2-2x3,
x2-2x3,又因为l-8x>0且x>0解得x的取值范围是(0,
 ).
).(Ⅱ)求出V′=
 x-6x2=-6x(x-
x-6x2=-6x(x-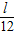 ),
),在(0,
 )上,V′>0,函数单调递增;在(
)上,V′>0,函数单调递增;在(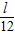 ,
, )上,V′<0,函数单调递减.
)上,V′<0,函数单调递减.∴当x=
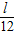 时,V取最大值.
时,V取最大值.此时,正四棱柱的高为
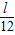 ,于是当正四棱柱底面边长和高之比是1时,其体积最大.
,于是当正四棱柱底面边长和高之比是1时,其体积最大.点评:考查学生会根据实际问题选择合适的函数类型,掌握棱柱的体积公式,会利用导数求闭区间上函数的最值.

练习册系列答案
相关题目
 (2013•营口二模)如图,用一根铁丝折成一个扇形框架,要求框架所围扇形面积为定值S,半径为r,弧长为l,则使用铁丝长度最小值时应满足的条件为( )
(2013•营口二模)如图,用一根铁丝折成一个扇形框架,要求框架所围扇形面积为定值S,半径为r,弧长为l,则使用铁丝长度最小值时应满足的条件为( )