Question

(理)已知函数f(x)=x²+lnx+(a-4)x在(1,+∞)上是增函数.

(1)求实数a的取值范围;

(2)在(1)的结论下,设g(x)=|e^x-a|+,x∈［0,ln3］,求函数g(x)的最小值.

(文)已知函数f(x)=x³+ax²+bx+c,g(x)=12x-4,若f(-1)=0,且f(x)的图象在点(1,f(1))处的切线方程为y=g(x).

(1)求实数a、b、c的值;

(2)求函数h(x)=f(x)-g(x)的单调区间.

Answer 1

答案：(理)解:(1)f′(x)=x++a-4.

∵f(x)在(1,+∞)上是增函数,∴x++a-4≥0在(1,+∞)上恒成立,即a≥4-(x+)恒成立.∵x+≥2(当且仅当x=1时,等号成立),∴4-(x+)＜2.∴a≥2.

(2)设t=e^x,则h(t)=|t-a|+.∵0≤x≤ln3,∴1≤t≤3.当2≤a≤3时,h(t)=

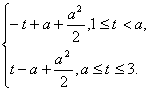
∴h(t)的最小值为h(a)=.

当a＞3时,h(t)=-t+a+.∴h(t)的最小值为h(3)=a-3+.

∴当2≤a≤3时,g(x)的最小值为;当a＞3时,g(x)的最小值为a-3+.

(文)解:(1)∵f(-1)=0,∴-1+a-b+c=0.①

∵f′(x)=3x²+2ax+b,又f(x)的图象在点(1,f(1))处的切线方程为y=g(x),∴f(1)=g(1)=8,且f′(1)=12.

即a+b+c=7,②

2a+b=9.③

联立方程①②③,解得a=3,b=3,c=1.

(2)h(x)=f(x)-g(x)=x³+3x²-9x+5.h′(x)=3x²+6x-9=3(x+3)(x-1).

令h′(x)=0,得x=-3或x=1.

X	(-∞,-3)	-3	(-3,1)	1	(1,+∞)
f′(x)	+	0	-	0	+
f(x)	?	极大		极小

 

故h(x)的单调增区间为(-∞,-3),(1,+∞),单调减区间为(-3,1).