题目内容
设m∈N+,log2m的整数部分用F(m)表示,则F(1)+F(2)+…+F(1024)的值是
- A.8204
- B.8192
- C.9218
- D.8021
A
分析:先找到能使得log2m是整数的m,再找到介于相邻的两个这样的m值之间的整数的个数,分别求值相加即可
解答:由题意知F(1)+F(2)+F(3)+F(4)+F(5)+F(6)+F(7)+F(8)+…+F(1024)=F(1)+F(2)+F(2)+F(4)+F(4)+F(4)+F(4)+F(8)+…+F(1024)
=(0+1×2+2×22+3×23+4×24+…+9×29)+10
设S=1×2+2×22+3×23+4×24+…+9×29
则2S=1×22+2×23+3×24+…+8×29+9×210
∴两式相减得:-S=2+22+23+…+29-9×210=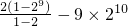 =-8×210-2
=-8×210-2
∴S=8×210+2
∴F(1)+F(2)+…+F(1024)=8×210+2+10=8204
故选A
点评:本题考察对数运算、错位相减法,要求对问题有较强的归纳分析能力和较好的运算能力.属中档题
分析:先找到能使得log2m是整数的m,再找到介于相邻的两个这样的m值之间的整数的个数,分别求值相加即可
解答:由题意知F(1)+F(2)+F(3)+F(4)+F(5)+F(6)+F(7)+F(8)+…+F(1024)=F(1)+F(2)+F(2)+F(4)+F(4)+F(4)+F(4)+F(8)+…+F(1024)
=(0+1×2+2×22+3×23+4×24+…+9×29)+10
设S=1×2+2×22+3×23+4×24+…+9×29
则2S=1×22+2×23+3×24+…+8×29+9×210
∴两式相减得:-S=2+22+23+…+29-9×210=
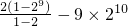 =-8×210-2
=-8×210-2∴S=8×210+2
∴F(1)+F(2)+…+F(1024)=8×210+2+10=8204
故选A
点评:本题考察对数运算、错位相减法,要求对问题有较强的归纳分析能力和较好的运算能力.属中档题

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
