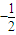题目内容
设数列{an}是各项均为正数的等比数列,Sn为其前n项和,m、n、p均为正整数,且满足m+n=2p,求证:
+
≥
.
| 1 | ||
|
| 1 | ||
|
| 2 | ||
|
分析:依题意,分q=1与q≠1讨论,利用分析法与基本不等式即可证得结论成立.
解答:解:当各项均为正数的等比数列{an}的公比q=1时,
+
=
+
=
(
+
)≥
×
,
∵m、n、p均为正整数,且满足m+n=2p,
∴2p≥2
,
∴
≤
,
∴
•
≤
•
,又
=
•
;
∴
+
≥
;
当q≠1时,
=
,
=
,
=
,
要证
+
≥
,只需证
+
≥
.
∵
+
≥
,
∴只需证(1-qm)•(1-qn)≤(1-qp)2,
即证-qm-qn+qm+n≤-2qp+q2p,∵m+n=2p,
∴只需证qm+qn≥2qp.
∵qm+qn≥2
=2
=2q
=2qp成立,
∴q≠1时,原结论成立.
综上所述,
+
≥
.
| 1 | ||
|
| 1 | ||
|
| 1 |
| (ma1)2 |
| 1 |
| (na1)2 |
| 1 |
| a12 |
| 1 |
| m2 |
| 1 |
| n2 |
| 1 |
| a12 |
| 2 |
| mn |
∵m、n、p均为正整数,且满足m+n=2p,
∴2p≥2
| mn |
∴
| 2 |
| p2 |
| 2 |
| mn |
∴
| 1 |
| a12 |
| 2 |
| p2 |
| 1 |
| a12 |
| 2 |
| mn |
| 2 | ||
|
| 1 |
| a12 |
| 2 |
| p2 |
∴
| 1 | ||
|
| 1 | ||
|
| 2 | ||
|
当q≠1时,
| 1 | ||
|
| (1-q)2 |
| a12(1-qm)2 |
| 1 | ||
|
| (1-q)2 |
| a12(1-qn)2 |
| 1 | ||
|
| (1-q)2 |
| a12(1-qp)2 |
要证
| 1 | ||
|
| 1 | ||
|
| 2 | ||
|
| 1 |
| (1-qm)2 |
| 1 |
| (1-qn)2 |
| 2 |
| (1-qp)2 |
∵
| 1 |
| (1-qm)2 |
| 1 |
| (1-qn)2 |
| 2 |
| (1-qm)(1-qn) |
∴只需证(1-qm)•(1-qn)≤(1-qp)2,
即证-qm-qn+qm+n≤-2qp+q2p,∵m+n=2p,
∴只需证qm+qn≥2qp.
∵qm+qn≥2
| qm•qn |
| qm+n |
| m+n |
| 2 |
∴q≠1时,原结论成立.
综上所述,
| 1 | ||
|
| 1 | ||
|
| 2 | ||
|
点评:本题考查等比数列的前n项和,突出分析法的应用,着重考查抽象思维与运算能力,考查逻辑推理与证明能力,属于难题.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
相关题目