题目内容
学校餐厅每天有500名学生就餐,每星期一有A,B两种套餐可选,每个学生任选一种,其中A是本校的传统套餐,B是从外校引人的套餐.调查资料表明,若在这星期一选A套餐的学生,下星期一会有
的学生改选B套餐;而选B套餐的学生,下周星期一会有r(0<r<
)的学生改选A套餐,用an,bn分别表示在第n个星期选A套餐的人数和选B套餐的人数.
(Ⅰ)用an-1表示an;
(Ⅱ)若r=
,且选A套餐的学生人数保持不变,求a1;
(Ⅲ)根据调查,存在一个常数k,使得数列{an-k}为等比数列,且k∈[250,300],求r的取值范围.
| 1 |
| 5 |
| 4 |
| 5 |
(Ⅰ)用an-1表示an;
(Ⅱ)若r=
| 3 |
| 10 |
(Ⅲ)根据调查,存在一个常数k,使得数列{an-k}为等比数列,且k∈[250,300],求r的取值范围.
分析:(Ⅰ)由已知得
,化简可用an-1表示an;
(Ⅱ)根据(Ⅰ)的结论,结合r=
,且选A套餐的学生人数保持不变,即可求a1;
(Ⅲ)根据数列{an-k}是等比数列,可用r表示k,根据k∈[250,300],即可求r的取值范围.
|
(Ⅱ)根据(Ⅰ)的结论,结合r=
| 3 |
| 10 |
(Ⅲ)根据数列{an-k}是等比数列,可用r表示k,根据k∈[250,300],即可求r的取值范围.
解答:解:(I)由已知得
,∴an=
an-1+r(500-an-1),
∴an=(
-r)an-1+500r. (4分)
(II)∵r=
,
∴an=
an-1+150=an-1
∴an-1=a1=300. (8分)
(III)∵数列{an-k}是等比数列,
∴an-k=
(an-1-k),得an=(
-r)an-1+(
+r)k,
∴(
+r)k=500r,得k=
,(11分)
∵k∈[250,300],∴250≤
≤300,
∴
≤r≤
. (13分)
|
| 4 |
| 5 |
∴an=(
| 4 |
| 5 |
(II)∵r=
| 3 |
| 10 |
∴an=
| 1 |
| 2 |
∴an-1=a1=300. (8分)
(III)∵数列{an-k}是等比数列,
∴an-k=
| 4 |
| 5 |
| 4 |
| 5 |
| 1 |
| 5 |
∴(
| 1 |
| 5 |
| 2500r |
| 5r+1 |
∵k∈[250,300],∴250≤
| 2500r |
| 5r+1 |
∴
| 1 |
| 5 |
| 3 |
| 10 |
点评:本题考查数列知识在生产实际中的应用,理清题设中的数量关系,合理地运用数列知识进行求解是关键.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
 ,
, 分别表示在第n个星期选A的人数和选B的人数,如果
分别表示在第n个星期选A的人数和选B的人数,如果 ,求
,求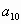 .
.