题目内容
已知函数f(x)是偶函数,且在区间[0,1]上是增函数,则f(-0.5),f(-1),f(0)的大小关系是________.
答案:f(0)<f(-0.5)<f(-1)
解析:
解析:
|
分析:-0.5,-1,0的大小显而易见,要得到对应的函数值的大小关系,需利用奇偶性将其自变量的值全转换到区间[0,1]内,再利用单调性即可得解. 解:因为函数f(x)是偶函数, 所以f(-0.5)=f(0.5),f(-1)=f(1). 又因为f(x)在区间[0,1]上是增函数, 所以f(0)<f(0.5)<f(1). 因此f(0)<f(-0.5)<f(-1). 点评:函数的单调性与奇偶性的综合应用是考查函数的重点.解决这类问题,也可利用数形结合迅速求解. |

练习册系列答案
相关题目

 (理)已知函数
(理)已知函数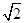 ]上的最小值.
]上的最小值.