题目内容
12.设点P是圆x2+y2=4上任意一点,由点P向x轴作垂线PP0,垂足为P0,且$\overrightarrow{M{P}_{0}}$=$\frac{\sqrt{3}}{2}$$\overrightarrow{P{P}_{0}}$,求点M的轨迹方程,并说明轨迹是什么.分析 利用中点坐标公式,确定P,M坐标之间的关系,将P的坐标代入圆的方程,即可求得M的轨迹方程.
解答 解:设M(x,y),P(m,n),则
∵由点P向x轴作垂线PP0,垂足为P0,且$\overrightarrow{M{P}_{0}}$=$\frac{\sqrt{3}}{2}$$\overrightarrow{P{P}_{0}}$,
∴m=x,n=-$\frac{2}{\sqrt{3}}$y
∵P在圆x2+y2=4上,
∴x2+$\frac{4}{3}$y2=4,
∴$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}$=1.
轨迹是焦点为(±1,0),长轴长为4的椭圆.
点评 本题考查轨迹方程,考查代入法的运用,考查学生的计算能力,确定坐标之间的关系是关键.

练习册系列答案
相关题目
2.设函数f(x)=x3-6x2+16x-5-sinπx,{an}是公差不为零的等差数列,若$\sum_{i=1}^{10}$f(ai)=110,则$\sum_{i=1}^{10}$ai=( )
| A. | 5 | B. | 10 | C. | 15 | D. | 20 |
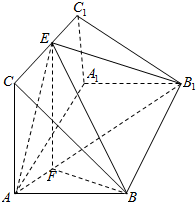 如图,是直三棱柱ABC-A1B1C1中,AA1=6,AB=AC=4,AB⊥AC,点E,F分别是AB1,CC1动点,$\overrightarrow{AF}$=λ$\overrightarrow{F{B}_{1}}$,$\overrightarrow{CE}$=μ$\overrightarrow{E{C}_{1}}$.则当V${\;}_{三棱锥{B}_{1}-EFB}$=4时,必有( )
如图,是直三棱柱ABC-A1B1C1中,AA1=6,AB=AC=4,AB⊥AC,点E,F分别是AB1,CC1动点,$\overrightarrow{AF}$=λ$\overrightarrow{F{B}_{1}}$,$\overrightarrow{CE}$=μ$\overrightarrow{E{C}_{1}}$.则当V${\;}_{三棱锥{B}_{1}-EFB}$=4时,必有( )