题目内容
椭圆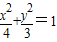 内有一点P(1,1),F为右焦点,椭圆上的点M使得MP+2MF的值最小,则点M的坐标为 .
内有一点P(1,1),F为右焦点,椭圆上的点M使得MP+2MF的值最小,则点M的坐标为 .
【答案】分析:由椭圆的第二定义可知,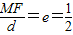 可得d=2MF,从而有|PM|+2|MF|=d+|PM|由题意可得,过P作PN⊥l,当M为该垂线与椭圆的右交点时,所求的值最小.
可得d=2MF,从而有|PM|+2|MF|=d+|PM|由题意可得,过P作PN⊥l,当M为该垂线与椭圆的右交点时,所求的值最小.
解答:解:∵椭圆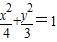 的a=2,b=
的a=2,b=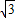 ,c=1,e=
,c=1,e= .
.
由题意可得点P在椭圆内部,设M到椭圆的左准线l得距离为d
由椭圆的第二定义可知,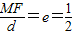 ,
,
∴d=2MF,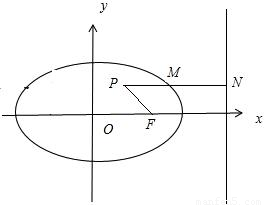
∴|PM|+2|MF|=d+|PM|
由题意可得,过P作PN⊥l,当M为该垂线与椭圆的右交点时,所求的值最小,
此时 yM=1,代入可得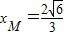
故答案为: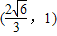 .
.
点评:本题主要考查了椭圆的第二定义的应用,解题得关键是灵活利用定义转化可得|PM|+2|MF|=d+|PM|,从而结合图象可求,体现了数形结合的思想的应用.
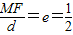 可得d=2MF,从而有|PM|+2|MF|=d+|PM|由题意可得,过P作PN⊥l,当M为该垂线与椭圆的右交点时,所求的值最小.
可得d=2MF,从而有|PM|+2|MF|=d+|PM|由题意可得,过P作PN⊥l,当M为该垂线与椭圆的右交点时,所求的值最小.解答:解:∵椭圆
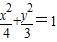 的a=2,b=
的a=2,b=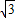 ,c=1,e=
,c=1,e= .
.由题意可得点P在椭圆内部,设M到椭圆的左准线l得距离为d
由椭圆的第二定义可知,
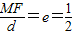 ,
,∴d=2MF,

∴|PM|+2|MF|=d+|PM|
由题意可得,过P作PN⊥l,当M为该垂线与椭圆的右交点时,所求的值最小,
此时 yM=1,代入可得
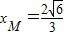
故答案为:
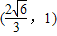 .
.点评:本题主要考查了椭圆的第二定义的应用,解题得关键是灵活利用定义转化可得|PM|+2|MF|=d+|PM|,从而结合图象可求,体现了数形结合的思想的应用.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案
相关题目
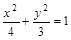 内有一点P(1,-1),F为椭圆右焦点,在椭圆上有一点M,使|MP|+2|MF|的值最小,则这一最小值是 ( )
内有一点P(1,-1),F为椭圆右焦点,在椭圆上有一点M,使|MP|+2|MF|的值最小,则这一最小值是 ( ) B.
B. C.3 D.4
C.3 D.4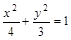 内有一点P(1,-1),F为椭圆右焦点,在椭圆上有一点M,使|MP|+2|MF|的值最小,则这一最小值是 ( )
内有一点P(1,-1),F为椭圆右焦点,在椭圆上有一点M,使|MP|+2|MF|的值最小,则这一最小值是 ( )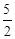 B.
B.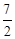 C.3 D.4
C.3 D.4 内有一点P(1,-1),F为椭圆右焦点,在椭圆上有一点M,使|MP|+2|MF|的值最小,则M的坐标 .
内有一点P(1,-1),F为椭圆右焦点,在椭圆上有一点M,使|MP|+2|MF|的值最小,则M的坐标 .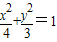 内有一点P(1,-1),F是椭圆的右焦点.
内有一点P(1,-1),F是椭圆的右焦点.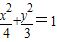 内有一点P(1,1),F为右焦点,椭圆上的点M使得MP+2MF的值最小,则点M的坐标为 .
内有一点P(1,1),F为右焦点,椭圆上的点M使得MP+2MF的值最小,则点M的坐标为 .