题目内容
在椭圆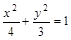 内有一点P(1,-1),F为椭圆右焦点,在椭圆上有一点M,使|MP|+2|MF|的值最小,则这一最小值是 ( )
内有一点P(1,-1),F为椭圆右焦点,在椭圆上有一点M,使|MP|+2|MF|的值最小,则这一最小值是 ( )
A.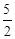 B.
B.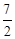 C.3 D.4
C.3 D.4
【答案】
C
【解析】主要考查椭圆的第二定义、椭圆的几何性质。
解:该椭圆的离心率为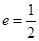 ,右准线为
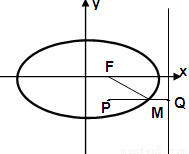
,右准线为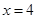 。过M点作MQ垂直于椭圆的右准线,垂足为点Q,由椭圆的第二定义可知:
。过M点作MQ垂直于椭圆的右准线,垂足为点Q,由椭圆的第二定义可知: 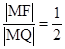 ,所以|MF|=
,所以|MF|= 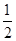 |MQ|,故|MP|+2|MF|=|MP|+|MQ|,
|MQ|,故|MP|+2|MF|=|MP|+|MQ|,
所以当P、M、Q三点共线时,|PQ|最小。由P(1,-1)得,
所求的值最小为|PQ|==4-1=3,故选C。

练习册系列答案
相关题目
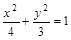 内有一点P(1,-1),F为椭圆右焦点,在椭圆上有一点M,使|MP|+2|MF|的值最小,则这一最小值是 ( )
内有一点P(1,-1),F为椭圆右焦点,在椭圆上有一点M,使|MP|+2|MF|的值最小,则这一最小值是 ( ) B.
B. C.3 D.4
C.3 D.4 内有一点P(1,-1),F为椭圆右焦点,在椭圆上有一点M,使|MP|+2|MF|的值最小,则此最小值是
内有一点P(1,-1),F为椭圆右焦点,在椭圆上有一点M,使|MP|+2|MF|的值最小,则此最小值是

 内有一点P(1,-1),F为椭圆右焦点,在椭圆上有一点M,使|MP|+2|MF|的值最小,则M的坐标 .
内有一点P(1,-1),F为椭圆右焦点,在椭圆上有一点M,使|MP|+2|MF|的值最小,则M的坐标 .