��Ŀ����
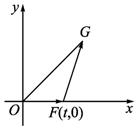
��OΪԭ�㣬(1)��x0����t�ĺ���x0=f(x)�ı���ʽ���жϺ���f(t)�ĵ����ԣ���֤������жϣ�
(2)���OFG�����S=![]() t������OΪ���ģ�FΪ�������Բ������G����|
t������OΪ���ģ�FΪ�������Բ������G����|![]() |ȡ����Сֵʱ��Բ�ķ��̣�
|ȡ����Сֵʱ��Բ�ķ��̣�
(3)��(2)�������£�����P������Ϊ(0��92)��C��D����Բ�ϵ����㣬��![]() =��
=��![]() (�ˡ�1)����ʵ���˵�ȡֵ��Χ.
(�ˡ�1)����ʵ���˵�ȡֵ��Χ.
�⣺(1)�����⣬![]() =(x0-t��y0)��
=(x0-t��y0)��![]() =(t��0)��
=(t��0)��
��![]() ��
��![]() =t(x0-t)=1����x0=f(t)=t+
=t(x0-t)=1����x0=f(t)=t+![]() .
.
��3��t1��t2����f(t2)-f(t1)=(t2+![]() )-(t1+
)-(t1+![]() )=
)=![]() .
.
��t2-t1��0��t1t2-1��0��t1t2��0����f(t2)-f(t1)��0��f(t2)��f(t1)��
��f(t)�ڣ�3��+��)�ϵ�������.
(2)��S=![]() |
|![]() ||y0|=
||y0|=![]() t��|y0|=
t��|y0|=![]() t����y0=��
t����y0=��![]() ��
��
���G������Ϊ(t+![]() ����
����![]() )��|
)��|![]() |2=(t+
|2=(t+![]() )2+
)2+![]() .
.
��f(t)�ڣ�3��+�ޣ��ϵ���������
�൱t=3ʱ��|![]() |ȡ����Сֵ����ʱF��G������ֱ���(3��0)��(
|ȡ����Сֵ����ʱF��G������ֱ���(3��0)��(![]() ����
����![]() ).
).
����������Բ����Ϊ![]() =1���ɵ�G����Բ�ϵ�
=1���ɵ�G����Բ�ϵ�![]() =1�����b2=9��
=1�����b2=9��
��������Բ����Ϊ![]() =1.
=1.
(3)����1����C��D������ֱ�Ϊ(x��y)��(m��n)����![]() =(x��y-
=(x��y-![]() )��
)��![]() =(m��n-
=(m��n-![]() ).
).
��![]() =��
=��![]() ����(x��y-
����(x��y-![]() )=��(m��n-
)=��(m��n-![]() )��x=��m��y=��n-
)��x=��m��y=��n-![]() ��+
��+![]() .
.
��C��D����Բ�ϣ���![]() =1��
=1��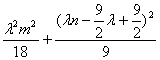 =1����ȥm�� n=
=1����ȥm�� n=![]() .
.
�֡�|n|��3����|![]() |��3�����
|��3�����![]() �ܦˡ�5����ʵ���˵�ȡֵ��Χ�ǣ�
�ܦˡ�5����ʵ���˵�ȡֵ��Χ�ǣ�![]() ��1)��(1��5��.
��1)��(1��5��.
����2���ǵ�A��B������ֱ�Ϊ(0��3)��(0��-3)������A��B�ֱ���y��Ĵ��ߣ���ֱ��PC�ڵ�M��N.
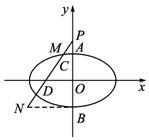
��|![]() |��|
|��|![]() |����|
|����|![]() |��|
|��|![]() |��|
|��|![]() |��|
|��|![]() |��
|��
��1��![]() ��
��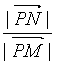 =
=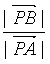 =5����1��
=5����1��![]() ��5��
��5��![]() �ܦˣ�1��
�ܦˣ�1��
��|![]() |��|
|��|![]() |��ͬ���ɵ�1��
|��ͬ���ɵ�1��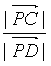 ��
��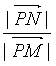 =
=![]() =5����1���ˡ�5.
=5����1���ˡ�5.
���ϣ�ʵ���˵�ȡֵ��Χ�ǣ�![]() ��1)��(1��5��.
��1)��(1��5��.

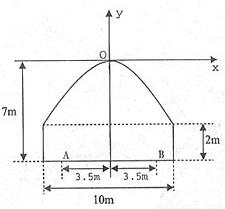
 ��ͼ��ʾ��һ��������˫���߹�·��������ɳ����ε������ߺ������ߵ�һ�ι��ɣ�Ϊ��֤��ȫ��Ҫ����ʻ������������Ϊƽ������������������ֱ�����ϸ߶�֮������Ҫ��0.5�ף�
��ͼ��ʾ��һ��������˫���߹�·��������ɳ����ε������ߺ������ߵ�һ�ι��ɣ�Ϊ��֤��ȫ��Ҫ����ʻ������������Ϊƽ������������������ֱ�����ϸ߶�֮������Ҫ��0.5�ף�