题目内容
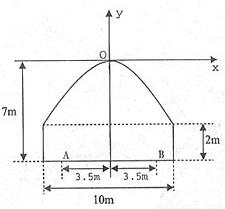
如图所示,一隧道内设双行线公路,其截面由长方形的三条边和抛物线的一段构成,为保证安全,要求行驶车辆顶部(设为平顶)与隧道顶部在竖直方向上高度之差至少要有0.5米.(1)以抛物线的顶点为原点O,其对称轴所在的直线为y轴,建立平面直角坐标系(如图),求该抛物线的方程;
(2)若行车道总宽度AB为7米,请计算通过隧道的车辆限制高度为多少米?(精确到0.1m)
【答案】分析:(1)依题意,选择合适的抛物线解析式x2=-2py(p>0)把有关数据转化为相应点的坐标,即可求得抛物线的方程;
(2)设车辆高h,则得出D(3.5,h-6.5)利用(1)的方程,将点的坐标代入方程x2=-5y,即可求出车辆通过隧道的限制高度.
解答: 解:如图所示
解:如图所示
(1)依题意,设该抛物线的方程为
x2=-2py(p>0)
因为点C(5,-5)在抛物线上,
所以该抛物线的方程为
x2=-5y
(2)设车辆高h,则|DB|=h+0.5
故D(3.5,h-6.5)
代入方程x2=-5y,
解得h=4.05
答:车辆通过隧道的限制高度为4.0米.
点评:本题主要考查了二次函数的应用,在解题时要通过题意画出图形,再根据所给的知识点求出答案是本题的关键.
(2)设车辆高h,则得出D(3.5,h-6.5)利用(1)的方程,将点的坐标代入方程x2=-5y,即可求出车辆通过隧道的限制高度.
解答:
 解:如图所示
解:如图所示(1)依题意,设该抛物线的方程为
x2=-2py(p>0)
因为点C(5,-5)在抛物线上,
所以该抛物线的方程为
x2=-5y
(2)设车辆高h,则|DB|=h+0.5
故D(3.5,h-6.5)
代入方程x2=-5y,
解得h=4.05
答:车辆通过隧道的限制高度为4.0米.
点评:本题主要考查了二次函数的应用,在解题时要通过题意画出图形,再根据所给的知识点求出答案是本题的关键.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
 如图所示,一隧道内设双行线公路,其截面由一段圆弧和一个长方形构成.已知隧道总宽度AD为
如图所示,一隧道内设双行线公路,其截面由一段圆弧和一个长方形构成.已知隧道总宽度AD为 如图所示,一隧道内设双行线公路,其截面由长方形的三条边和抛物线的一段构成,为保证安全,要求行驶车辆顶部(设为平顶)与隧道顶部在竖直方向上高度之差至少要有0.5米.
如图所示,一隧道内设双行线公路,其截面由长方形的三条边和抛物线的一段构成,为保证安全,要求行驶车辆顶部(设为平顶)与隧道顶部在竖直方向上高度之差至少要有0.5米.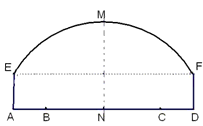 如图所示,一隧道内设双行线公路,其截面由一段圆弧和一个长方形构成.已知隧道总宽度AD为
如图所示,一隧道内设双行线公路,其截面由一段圆弧和一个长方形构成.已知隧道总宽度AD为 m,行车道总宽度BC为
m,行车道总宽度BC为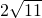 m,侧墙EA、FD高为2m,弧顶高MN为5m.
m,侧墙EA、FD高为2m,弧顶高MN为5m.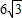 m,行车道总宽度BC为
m,行车道总宽度BC为 m,侧墙EA、FD高为2m,弧顶高MN为5m.
m,侧墙EA、FD高为2m,弧顶高MN为5m.