题目内容
将边长为2,一个内角为60°的菱形ABCD沿较短对角线BD折成四面体ABCD,点E、F分别为AC、BD 的中点,则下列命题中正确是
①EF与AC和BD都垂直; ②EF∥AB;
③AC垂直于截面BDE; ④当四面体ABCD的体积最大时,AC=
.
①③④
①③④
(填上你认为正确的所有答案序号)①EF与AC和BD都垂直; ②EF∥AB;
③AC垂直于截面BDE; ④当四面体ABCD的体积最大时,AC=
| 6 |
分析:画出图形,利用翻折前后线面关系,角的关系,逐一分析各个选项的正确性,把正确的选项找出来.
解答:解:由等腰三角形的中线性质得 CF⊥BD,AF⊥BD,DB⊥面ACF,又EF?面ACF,
∴EF⊥BD,且EF⊥AC,故①正确;
如图:由题意得,EF与AB是异面直线,故②不正确;
由DB⊥面ACF 得,DB⊥AC,又EF⊥AC,∴AC⊥面EBD,故③正确;
当四面体ABCD的体积最大时,因为等边△ABD的面积为定值,
故面SBD⊥面ABD,CF为四面体的高,
AC=
=
=
,故④正确.
故答案为:①③④.

∴EF⊥BD,且EF⊥AC,故①正确;
如图:由题意得,EF与AB是异面直线,故②不正确;
由DB⊥面ACF 得,DB⊥AC,又EF⊥AC,∴AC⊥面EBD,故③正确;
当四面体ABCD的体积最大时,因为等边△ABD的面积为定值,
故面SBD⊥面ABD,CF为四面体的高,
AC=
| CF2+FA2 |
| 3+3 |
| 6 |
故答案为:①③④.
点评:本题考查棱锥的结构特征,注意在翻折过程中哪些量发生了变化,哪些量没有发生变化;位于折线同侧的元素关系不变,位于折线两侧的元素关系会发生变化.

练习册系列答案
相关题目
 的菱形
的菱形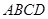 沿较短对角线
沿较短对角线 折成四面体
折成四面体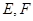 分别为
分别为 的中点,则下列命题中正确的是
。
的中点,则下列命题中正确的是
。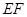 ∥
∥ ;②
;② ;③
;③ ;
⑤
;
⑤ 垂直于截面
垂直于截面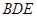 .
. 的菱形
的菱形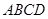 沿较短对角线
沿较短对角线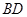 折成四面体
折成四面体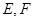 分别为
分别为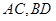 的中点,则下列命题中正确的是
的中点,则下列命题中正确的是
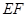 ∥
∥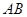 ;②
;②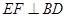 ;③
;③ ;
⑤
;
⑤ 垂直于截面
垂直于截面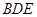 .
. ;
;