题目内容
设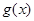 是定义在
是定义在 上,且以1为周期的函数,若函数
上,且以1为周期的函数,若函数 在区间
在区间 上的值域为
上的值域为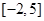 ,则
,则 在区间
在区间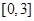 上的值域为________.
上的值域为________.
【答案】
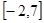
【解析】解:g(x)为R上周期为1的函数,则g(x)=g(x+1)函数f(x)=x+g(x)在区间[0,1]【正好是一个周期区间长度】的值域是[-2,5]
令x+1=t,当x∈[0,1]时,t=x+1∈[1,2]
此时,f(t)=t+g(t)=(x+1)+g(x+1)=(x+1)+g(x)
=[x+g(x)]+1
所以,在t∈[1,2]时,f(t)∈[-1,6]…(1)
同理,令x+2=t,在当x∈[0,1]时,t=x+2∈[2,3]
此时,f(t)=t+g(t)=(x+2)+g(x+2)=(x+2)+g(x)
=[x+g(x)]+2
所以,当t∈[2,3]时,f(t)∈[0,7]…(2)
由已知条件及(1)(2)得到,f(x)在区间[0,3]上的值域为[-2,7]
故答案为:[-2,7].

练习册系列答案
相关题目
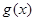 是定义在
是定义在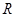 上且以1为周期的函数,若函数
上且以1为周期的函数,若函数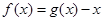 在区间
在区间 上的值域为
上的值域为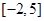 ,则
,则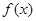 在区间
在区间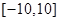 上的值域为
上的值域为