题目内容
已知f(x)=rx-xr(x>0),其中r是区间(0,1)上的常数,则f(x)的单调增区间为 .
【答案】分析:已知f(x)=rx-xr(x>0),其中r是区间(0,1)上的常数,其单调增函数,说明f′(x)大于0,从而解出f(x)的单调增区间;
解答:解:∵f(x)=rx-xr(x>0),
f′(x)=r-rxr-1=r(1-xr-1)=r(1-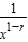 ),0<1-r<1,
),0<1-r<1,
求f(x)单调增区间,
∴f′(x)=r(1- )>0,r>0,
)>0,r>0,
∴0<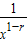 <1,0<1-r<1,
<1,0<1-r<1,
∴x>1,
∴f(x)的单调增区间为(1,+∞);
故答案为:(1,+∞);
点评:本题主要考查导函数的正负与原函数的单调性之间的关系,即当导函数大于0时原函数单调递增,当导函数小于0时原函数单调递减,是一道基础题;
解答:解:∵f(x)=rx-xr(x>0),
f′(x)=r-rxr-1=r(1-xr-1)=r(1-
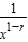 ),0<1-r<1,
),0<1-r<1,求f(x)单调增区间,
∴f′(x)=r(1-
 )>0,r>0,
)>0,r>0,∴0<
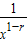 <1,0<1-r<1,
<1,0<1-r<1,∴x>1,
∴f(x)的单调增区间为(1,+∞);
故答案为:(1,+∞);
点评:本题主要考查导函数的正负与原函数的单调性之间的关系,即当导函数大于0时原函数单调递增,当导函数小于0时原函数单调递减,是一道基础题;

练习册系列答案
相关题目