题目内容
已知动圆C经过点(0,m)(m>0),且与直线y=-m相切,圆C被x轴截得弦长的最小值为1.记该圆圆心的轨迹为E.(Ⅰ)求曲线E的方程;
(Ⅱ)是否存在曲线C与曲线E的一个公共点,使它们在该点处有相同的切线?若存在,求出切线方程;若不存在,说明理由.
【答案】分析:(Ⅰ)先设出曲线E的方程,再确定圆的方程,利用圆C被x轴截得弦长的最小值为1,即可求曲线E的方程;
(Ⅱ)假设存在题设的公共点B,代入圆的方程并整理,求导确定切线斜率,利用圆切线的性质可得方程,联立方程,即可求出切线方程.
解答:解:(Ⅰ)依题意,曲线E是以(0,m)为焦点,以y=-m为准线的抛物线,所以曲线E的方程为x2=4my.…(2分)
设动圆圆心为A(a,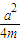 ),则圆C方程为(x-a)2+(y-
),则圆C方程为(x-a)2+(y-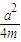 )2=(
)2=(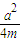 +m)2,
+m)2,
令y=0,得(x-a)2= +m2.
+m2.
当a=0时,圆C被x轴截得弦长取得最小值2m,于是m= ,故曲线E的方程为x2=2y.…(5分)
,故曲线E的方程为x2=2y.…(5分)
(Ⅱ)假设存在题设的公共点B(b, b2).
b2).
圆C方程为(x-a)2+(y- a2)2=(
a2)2=( a2+
a2+ )2,
)2,
将点B坐标代入上式,并整理,得(b-a)2[1+ (a+b)2]=
(a+b)2]= (a2+1)2.①…(7分)
(a2+1)2.①…(7分)
对y= x2求导,得y′=x,则曲线E在点B处的切线斜率为b.
x2求导,得y′=x,则曲线E在点B处的切线斜率为b.
又直线AB的斜率k=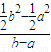 =
= (a+b).
(a+b).
由圆切线的性质,有 (a+b)b=-1.②…(8分)
(a+b)b=-1.②…(8分)
由①和②得b2(b2-8)=0.
显然b≠0,则b=±2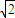 .…(9分)
.…(9分)
所以存在题设的公共点B,其坐标为(±2 ,4),公切线方程为y=2
,4),公切线方程为y=2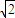 (x-2
(x-2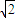 )+4或y=-2
)+4或y=-2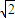 (x+2
(x+2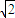 )+4,即y=±2
)+4,即y=±2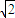 x-4.…(12分)
x-4.…(12分)
点评:本题考查轨迹方程,考查直线与圆的位置关系,考查学生分析解决问题的能力,考查学生的计算能力,属于中档题.
(Ⅱ)假设存在题设的公共点B,代入圆的方程并整理,求导确定切线斜率,利用圆切线的性质可得方程,联立方程,即可求出切线方程.
解答:解:(Ⅰ)依题意,曲线E是以(0,m)为焦点,以y=-m为准线的抛物线,所以曲线E的方程为x2=4my.…(2分)
设动圆圆心为A(a,
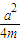 ),则圆C方程为(x-a)2+(y-
),则圆C方程为(x-a)2+(y-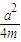 )2=(
)2=(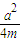 +m)2,
+m)2,令y=0,得(x-a)2=
 +m2.
+m2.当a=0时,圆C被x轴截得弦长取得最小值2m,于是m=
 ,故曲线E的方程为x2=2y.…(5分)
,故曲线E的方程为x2=2y.…(5分)(Ⅱ)假设存在题设的公共点B(b,
 b2).
b2).圆C方程为(x-a)2+(y-
 a2)2=(
a2)2=( a2+
a2+ )2,
)2,将点B坐标代入上式,并整理,得(b-a)2[1+
 (a+b)2]=
(a+b)2]= (a2+1)2.①…(7分)
(a2+1)2.①…(7分)对y=
 x2求导,得y′=x,则曲线E在点B处的切线斜率为b.
x2求导,得y′=x,则曲线E在点B处的切线斜率为b.又直线AB的斜率k=
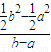 =
= (a+b).
(a+b).由圆切线的性质,有
 (a+b)b=-1.②…(8分)
(a+b)b=-1.②…(8分)由①和②得b2(b2-8)=0.
显然b≠0,则b=±2
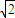 .…(9分)
.…(9分)所以存在题设的公共点B,其坐标为(±2
 ,4),公切线方程为y=2
,4),公切线方程为y=2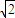 (x-2
(x-2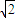 )+4或y=-2
)+4或y=-2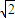 (x+2
(x+2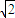 )+4,即y=±2
)+4,即y=±2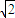 x-4.…(12分)
x-4.…(12分)点评:本题考查轨迹方程,考查直线与圆的位置关系,考查学生分析解决问题的能力,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目