题目内容
(1)求在极坐标系中,以(2,
)为圆心,2为半径的圆的参数方程;
(2)将参数方程
(θ为参数) 化为直角坐标方程.
| π |
| 2 |
(2)将参数方程
|
分析:(1)在对应的直角坐标系中,求出圆的直角坐标方程,再依据x=ρcosθ,y=ρsinθ,把直角坐标方程化为极坐标方程.
(2)由条件并利用 cos2θ=1-2sin2θ,可得 y=-2x2,-1≤x≤1.
(2)由条件并利用 cos2θ=1-2sin2θ,可得 y=-2x2,-1≤x≤1.
解答:解:(1)在对应的直角坐标系中,圆心的坐标为(0,2),圆的直角坐标方程为 x2+(y-2)2=4,
圆的参数方程为:
(θ为参数).
(2)因为cos2θ=1-2sin2θ,∴y+1=1-2x2,
即:y=-2x2 (-1≤x≤1),
故答案为:y=-2x2,(-1≤x≤1).
圆的参数方程为:
|
(2)因为cos2θ=1-2sin2θ,∴y+1=1-2x2,
即:y=-2x2 (-1≤x≤1),
故答案为:y=-2x2,(-1≤x≤1).
点评:(1)本题考查求圆的极坐标方程的方法,极坐标方程化为普通方程的方法,利用x=ρcosθ,y=ρsinθ,把直角坐标方程化为极坐标方程,
(20本题考查二倍角的余弦公式,把参数方程化为普通方程的方法,利用cos2θ=1-2sin2θ,是解题的关键.
(20本题考查二倍角的余弦公式,把参数方程化为普通方程的方法,利用cos2θ=1-2sin2θ,是解题的关键.

练习册系列答案
相关题目
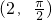 为圆心,2为半径的圆的参数方程;
为圆心,2为半径的圆的参数方程;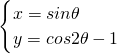 (θ为参数) 化为直角坐标方程.
(θ为参数) 化为直角坐标方程.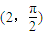 为圆心,2为半径的圆的参数方程;
为圆心,2为半径的圆的参数方程;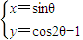 (θ为参数) 化为直角坐标方程.
(θ为参数) 化为直角坐标方程.