题目内容
(1)求该同学在第一个交通岗遇到红灯,其它交通岗未遇到红灯的概率;
(2)若
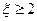 ,则该同学就迟到,求该同学不迟到的概率;
,则该同学就迟到,求该同学不迟到的概率;(3)求随机变量
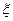 的数学期望和方差
的数学期望和方差(1)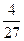 ;(2)
;(2)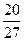 ;(3)
;(3)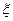 的数学期望为1,方差为
的数学期望为1,方差为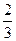
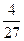 ;(2)
;(2)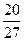 ;(3)
;(3)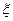 的数学期望为1,方差为
的数学期望为1,方差为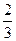
(1)用事件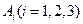 表示该同学在第
表示该同学在第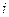 个交通岗遇到红灯,
个交通岗遇到红灯,
事件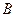 表示“在第一个交通岗遇到红灯,其它交通岗未遇到红灯”,……1分
表示“在第一个交通岗遇到红灯,其它交通岗未遇到红灯”,……1分
则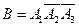 ,且事件
,且事件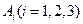 两两相互独立. …………2分
两两相互独立. …………2分
所以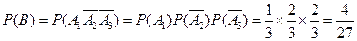 .……4分
.……4分
(2)因为该同学经过三个交通岗时,是否遇到红灯互不影响,所以可看成3次独立重复试验,
即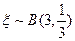 ……………………………………………………6分
……………………………………………………6分
所以该学生不迟到的概率为:
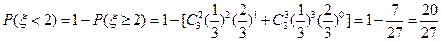 …8分
…8分
(3)因为随机变量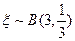 ………………………9分
………………………9分
所以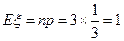 ,………………………………………10分
,………………………………………10分
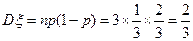 . ……………………………………………11分
. ……………………………………………11分
答:该同学恰好在第一个交通岗遇到红灯的概率为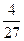 ;该同学不迟到的概率为
;该同学不迟到的概率为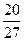 ;
;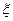 的数学期望为1,方差为
的数学期望为1,方差为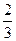 . ………………………………………12分
. ………………………………………12分
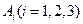 表示该同学在第
表示该同学在第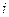 个交通岗遇到红灯,
个交通岗遇到红灯,事件
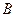 表示“在第一个交通岗遇到红灯,其它交通岗未遇到红灯”,……1分
表示“在第一个交通岗遇到红灯,其它交通岗未遇到红灯”,……1分则
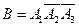 ,且事件
,且事件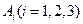 两两相互独立. …………2分
两两相互独立. …………2分所以
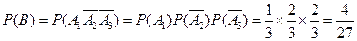 .……4分
.……4分(2)因为该同学经过三个交通岗时,是否遇到红灯互不影响,所以可看成3次独立重复试验,
即
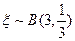 ……………………………………………………6分
……………………………………………………6分所以该学生不迟到的概率为:
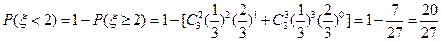 …8分
…8分(3)因为随机变量
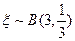 ………………………9分
………………………9分所以
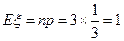 ,………………………………………10分
,………………………………………10分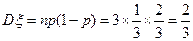 . ……………………………………………11分
. ……………………………………………11分答:该同学恰好在第一个交通岗遇到红灯的概率为
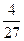 ;该同学不迟到的概率为
;该同学不迟到的概率为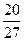 ;
;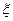 的数学期望为1,方差为
的数学期望为1,方差为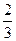 . ………………………………………12分
. ………………………………………12分
练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
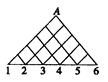
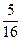
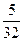
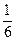
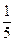
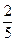
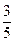
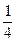
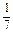 .现有甲、乙两人从袋中轮流摸球,甲先取,乙后取,然后甲再取……取后不放回,直到两人中有1人取到白球时即终止.每个球在每一次被取出的机会是等可能的.
.现有甲、乙两人从袋中轮流摸球,甲先取,乙后取,然后甲再取……取后不放回,直到两人中有1人取到白球时即终止.每个球在每一次被取出的机会是等可能的.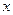 m的河流,该人不小心把一件物品丢在途中,若物品掉在河里就找不到,物品不掉在河里,则能找到,已知该物品能被找到的概率为
m的河流,该人不小心把一件物品丢在途中,若物品掉在河里就找不到,物品不掉在河里,则能找到,已知该物品能被找到的概率为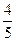 ,则河宽为( )
,则河宽为( )