题目内容
设数列{an}前n的项和为Sn,且(3-m)Sn+2man=m+3(n∈N*).其中m为常数,m≠-3且m≠0(1)求证:{an}是等比数列;
(2)若数列{an}的公比满足q=f(m)且b1=a1=1,bn=
| 3 |
| 2 |
| 1 |
| bn |
分析:(1)根据所给的关系式(3-m)Sn+2man=m+3,仿写一个关系式,两式相减,减掉了前n项和的形式,变成数列的递推式,得到连续两项的比值等于常数,证出是一个等比数列.
(2)根据所给的关于数列的关系式,看清题目的发展方向是求通项的倒数是一个等差数列,需要把关系式两边同时除以连续两项的积,得到结论,写出通项.
(2)根据所给的关于数列的关系式,看清题目的发展方向是求通项的倒数是一个等差数列,需要把关系式两边同时除以连续两项的积,得到结论,写出通项.
解答:解:(1)由(3-m)Sn+2man=m+3,得(3-m)Sn+1+2man+1=m+3,
两式相减,得(3+m)an+1=2man,(m≠-3)
∴
=
,
∴{an}是等比数列.
(2)由b1=a1=1,q=f(m)=
,
n∈N且n≥2时,bn=
f(bn-1)=
•
得
bnbn-1+3bn=3bn-1⇒
-
=
.
∴{
}是1为首项
为公差的等差数列,
∴
=1+
=
,故有bn=
.
两式相减,得(3+m)an+1=2man,(m≠-3)
∴
| an+1 |
| an |
| 2m |
| m+3 |
∴{an}是等比数列.
(2)由b1=a1=1,q=f(m)=
| 2m |
| m+3 |
n∈N且n≥2时,bn=
| 3 |
| 2 |
| 3 |
| 2 |
| 2bn-1 |
| bn-1+3 |
bnbn-1+3bn=3bn-1⇒
| 1 |
| bn |
| 1 |
| bn-1 |
| 1 |
| 3 |
∴{
| 1 |
| bn |
| 1 |
| 3 |
∴
| 1 |
| bn |
| n-1 |
| 3 |
| n+2 |
| 3 |
| 3 |
| n+2 |
点评:本题考查有递推式求通项,这是数列中常见的一种题目,在解题时注意要求证明数列是等比数列或等差数列,需要按照数列的定义来看题目的思路.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
 为等差数列,并求bn.
为等差数列,并求bn.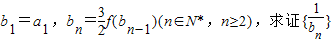 为等差数列,并求bn.
为等差数列,并求bn.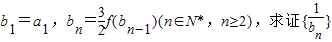 为等差数列,并求bn.
为等差数列,并求bn.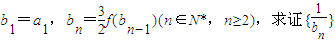 为等差数列,并求bn.
为等差数列,并求bn.