题目内容
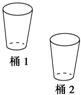 如图,开始时桶1中有a升水,如果桶1向桶2注水,桶1中剩余的水符合指数衰减曲线y1=a•e-nt(n为常数,t为注水时间),那么桶2中的水就是y2=a-a•e-nt.如果由桶1向桶2中注水5分钟时,两桶中的水相等,那么经过
如图,开始时桶1中有a升水,如果桶1向桶2注水,桶1中剩余的水符合指数衰减曲线y1=a•e-nt(n为常数,t为注水时间),那么桶2中的水就是y2=a-a•e-nt.如果由桶1向桶2中注水5分钟时,两桶中的水相等,那么经过15
15
分钟桶1中的水只有| a | 8 |
分析:由题意,根据5分钟后两桶水体积相等建立方程解出e-n的值,将其代入解析式,令函数值为
,解此方程即可计算出所需要的时间
| a |
| 8 |
解答:解:由于t=5时两桶中的水相等,所以a•e-n×5=a-a•e-n×5,
所以(e-n)5=
,即e-n×5=1-e-n×5,即e-n=(
)
由条件可得a•e-nt=
,即(
)
=(
)3,所以t=15.
即经过15分钟,桶1中的水只有
故答案为 15
所以(e-n)5=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 5 |
由条件可得a•e-nt=
| a |
| 8 |
| 1 |
| 2 |
| t |
| 5 |
| 1 |
| 2 |
即经过15分钟,桶1中的水只有
| a |
| 8 |
故答案为 15
点评:本题是指数函数应用题,根据实际问题建立方程与熟练掌握指数的运算性质是解答的关键

练习册系列答案
相关题目
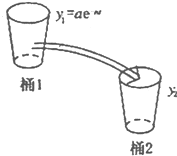 (2009•河北区二模)如图所示,桶1中的水按一定规律流入桶2中,已知开始时桶1中有a升水,桶2是空的,t分钟后桶1中剩余的水符合指数衰减曲线
(2009•河北区二模)如图所示,桶1中的水按一定规律流入桶2中,已知开始时桶1中有a升水,桶2是空的,t分钟后桶1中剩余的水符合指数衰减曲线 如图,开始时桶1中有a升水,如果桶1向桶2注水,桶1中剩余的水符合指数衰减曲线y1=a•e-nt(n为常数,t为注水时间),那么桶2中的水就是y2=a-a•e-nt.如果由桶1向桶2中注水5分钟时,两桶中的水相等,那么经过________分钟桶1中的水只有
如图,开始时桶1中有a升水,如果桶1向桶2注水,桶1中剩余的水符合指数衰减曲线y1=a•e-nt(n为常数,t为注水时间),那么桶2中的水就是y2=a-a•e-nt.如果由桶1向桶2中注水5分钟时,两桶中的水相等,那么经过________分钟桶1中的水只有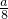 .
.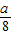 .
.
