题目内容
直线l与抛物线相交于A,B两点,F是抛物线的焦点.(1)求证:“如果直线l过点T(3,0),那么
| OA |
| OB |
(2)设A(x1,y1),B(x2,y2),D(x3,y3)是抛物线上三点,且|AF|,|BF|,|DF|成等差数列.当AD的垂直平分线与x轴交于点T(3,0)时,求点B的坐标.
分析:(1)设出A,B两点的坐标根据向量的点乘运算求证即可,(2)由|AF|,|BF|,|DF|成等差数列,则2|BF|=|AF|+|DF|,即,从而问题可解.
解答:解:(1)设过点T(3,0)的直线l交抛物线y2=4x于点A(x1,y1)、B(x2,y2).
当直线l的钭率不存在时,直线l的方程为x=3,
此时,直线l与抛物线相交于点A(3,2
)、B(3,-2
).
∴
=-3
当直线l的钭率存在时,设直线l的方程为y=k(x-3),其中k≠0,
由
得ky2-4y-12k=0⇒y1y2=-12
又∵x1=
y12,x2=
y22∴
=-3,
综上所述,命题“如果直线l过点T(3,0),那么
=-3”是真命题;
综上,命题成立.
(2)由|AF|,|BF|,|DF|成等差数列,则2|BF|=|AF|+|DF|,即2x2=x1+x3
直线AD斜率k=
=
所以y3+y1=
,设AD中点为(x2,
)
故AD的垂直平分线为y-
=-
(x-x2)
令y=0,得x=2+x2,∴x2=1,代入y2=4x得y=±2,故B(1,2)或B(1,-2)
当直线l的钭率不存在时,直线l的方程为x=3,
此时,直线l与抛物线相交于点A(3,2
| 3 |
| 3 |
∴
| OA |
| OB |
当直线l的钭率存在时,设直线l的方程为y=k(x-3),其中k≠0,
由
|
又∵x1=
| 1 |
| 4 |
| 1 |
| 4 |
| OA |
| OB |
综上所述,命题“如果直线l过点T(3,0),那么
| OA |
| OB |
综上,命题成立.
(2)由|AF|,|BF|,|DF|成等差数列,则2|BF|=|AF|+|DF|,即2x2=x1+x3
直线AD斜率k=
| y3-y1 |
| x3-x1 |
| 4 |
| y3+y1 |
所以y3+y1=
| 4 |
| k |
| 2 |
| k |
故AD的垂直平分线为y-
| 2 |
| k |
| 1 |
| k |
令y=0,得x=2+x2,∴x2=1,代入y2=4x得y=±2,故B(1,2)或B(1,-2)
点评:本题考查了真假命题的证明,但要知道向量点乘运算的知识.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
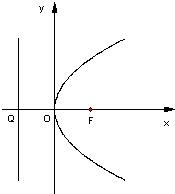 如图,F是抛物线y2=2px(p>0)的焦点,Q是准线与x轴的交点,斜率为k的直线l经过点Q.
如图,F是抛物线y2=2px(p>0)的焦点,Q是准线与x轴的交点,斜率为k的直线l经过点Q.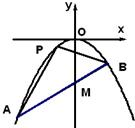 如图,抛物线的顶点O在坐标原点,焦点在y轴负半轴上.
如图,抛物线的顶点O在坐标原点,焦点在y轴负半轴上.