题目内容
设抛物线x2=12y的焦点为F,经过点P(-2,2)的直线l与抛物线相交于A、B两点,又点P恰为AB的中点,则|AF|+|BF|=
10
10
.分析:求出焦点坐标和准线方程,过A、B、P 作准线的垂线段,垂足分别为 M、N、R,利用抛物线的定义得到|AM|+|BN|=2|PR|,求得结果.
解答: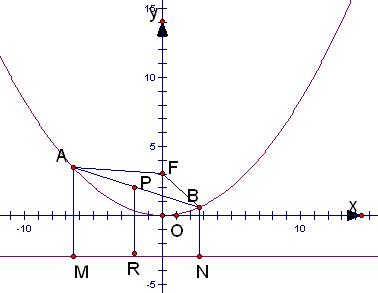 解:抛物线 x2=12y的焦点为F(0,3),准线方程为y=-3,过A、B、P 作准线的垂线段,垂足分别为 M、N、R,
解:抛物线 x2=12y的焦点为F(0,3),准线方程为y=-3,过A、B、P 作准线的垂线段,垂足分别为 M、N、R,
点P恰为AB的中点,故|PR|是直角梯形AMNP的中位线,故|AM|+|BN|=2|PR|.
由抛物线的定义可得|AF|+|BF|=|AM|+|BN|=2|PR|=2|2-(-3)|=10,
故答案为:10
 解:抛物线 x2=12y的焦点为F(0,3),准线方程为y=-3,过A、B、P 作准线的垂线段,垂足分别为 M、N、R,
解:抛物线 x2=12y的焦点为F(0,3),准线方程为y=-3,过A、B、P 作准线的垂线段,垂足分别为 M、N、R,点P恰为AB的中点,故|PR|是直角梯形AMNP的中位线,故|AM|+|BN|=2|PR|.
由抛物线的定义可得|AF|+|BF|=|AM|+|BN|=2|PR|=2|2-(-3)|=10,
故答案为:10
点评:本题考查抛物线的定义、标准方程,以及简单性质的应用,利用抛物线的定义得到|AM|+|BN|=2|PR|,是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目