题目内容
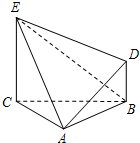 已知△ABC为正三角形,EC⊥平面ABC,DB⊥平面ABC,且EC,DB在平面ABC的同侧,CE=CA=2BD=2.
已知△ABC为正三角形,EC⊥平面ABC,DB⊥平面ABC,且EC,DB在平面ABC的同侧,CE=CA=2BD=2.(1)求证平面CAE⊥平面DAE;
(2)求:点B到平面ADE的距离.
分析:(1)由于N是EA的中点,容易得到DN∥BM,而BM⊥平面ECA,从而得证;
(2)直接根据VB-ADE=VE-ADB=VC-ADB,列出关于点B到平面ADE的距离的等式,即可求出结论.
(2)直接根据VB-ADE=VE-ADB=VC-ADB,列出关于点B到平面ADE的距离的等式,即可求出结论.
解答: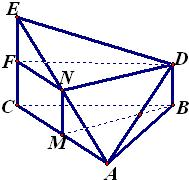
解:(1)证明:取AC中点M,取AE中点N,连接MN、MB,DN,
∵N是EA的中点,
∴MN=
EC.由BD=
EC,且BD⊥平面ABC,
可得四边形MNBD是矩形,于是DN∥BM.
∴DN⊥AC
∵CE=CA=2BD=2
∴可得DE=DA,N是EA的中点,
∴DN⊥EA.又EA∩MN=M,
∴DN⊥平面ECA,DN?平面DEA,
∴平面DEA⊥平面ECA.
(2):设点B到平面ADE的距离为h
∵△ABC为正三角形
∴C到AB的距离d=
,由BD⊥平面ABC可得C到AB的距离即为C到面ABD的距离,
∵VB-ADE=VE-ADB=VC-ADB.
∴
×
×DN•AE•h=
×S△ABD•d.
∴h=
=
=
=
=
=
.

解:(1)证明:取AC中点M,取AE中点N,连接MN、MB,DN,
∵N是EA的中点,
∴MN=
| 1 |
| 2 |
| 1 |
| 2 |
可得四边形MNBD是矩形,于是DN∥BM.
∴DN⊥AC
∵CE=CA=2BD=2
∴可得DE=DA,N是EA的中点,
∴DN⊥EA.又EA∩MN=M,
∴DN⊥平面ECA,DN?平面DEA,
∴平面DEA⊥平面ECA.
(2):设点B到平面ADE的距离为h
∵△ABC为正三角形
∴C到AB的距离d=
| 3 |
∵VB-ADE=VE-ADB=VC-ADB.
∴
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
∴h=
| AB•d•d |
| DN•AE |
| AB•d•d |
| BM•AE |
| AB•d•d |
| d•AE |
| AB•d |
| AE |
2×
| ||
|
| ||
| 2 |
点评:本题考查空间中平面与平面垂直的问题,面面垂直转化为线面垂直解决,同时注意使用线面垂直的判定定理及性质定理.

练习册系列答案
相关题目


