题目内容
(本小题满分 分)
分)
设函数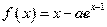 .
.
(Ⅰ)求函数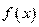 单调区间;
单调区间;
(Ⅱ)若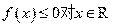 恒成立,求
恒成立,求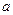 的取值范围;
的取值范围;
 分)
分)设函数
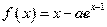 .
.(Ⅰ)求函数
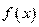 单调区间;
单调区间; (Ⅱ)若
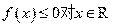 恒成立,求
恒成立,求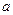 的取值范围;
的取值范围; 解:(I)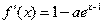
当 时,
时, ,
, 在
在 上是增函数;
上是增函数;
当 时,令
时,令 得
得 , ……………………3分
, ……………………3分
若 ,则
,则 ,从而
,从而 在区间
在区间 上是增函数;
上是增函数;
若 ,则
,则 ,从而
,从而 在区间
在区间 上是减函数.
上是减函数.
综上可知:当 时,
时, 在区间
在区间 上是增函数.当
上是增函数.当 时,在区间
时,在区间 上是增函数,
上是增函数, 在区间
在区间 上是减函数 …………6分
上是减函数 …………6分
(II)由(I)可知:当 时,
时, 不恒成立 …………8分
不恒成立 …………8分
又当 时,
时, 在点
在点 处取最大值,
处取最大值,
且 ………………10分
………………10分
令 得
得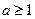
故若 对
对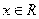 恒成立,则
恒成立,则 的取值范围是
的取值范围是  ……12分
……12分
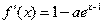
当
 时,
时, ,
, 在
在 上是增函数;
上是增函数;当
 时,令
时,令 得
得 , ……………………3分
, ……………………3分若
 ,则
,则 ,从而
,从而 在区间
在区间 上是增函数;
上是增函数;若
 ,则
,则 ,从而
,从而 在区间
在区间 上是减函数.
上是减函数.综上可知:当
 时,
时, 在区间
在区间 上是增函数.当
上是增函数.当 时,在区间
时,在区间 上是增函数,
上是增函数, 在区间
在区间 上是减函数 …………6分
上是减函数 …………6分(II)由(I)可知:当
 时,
时, 不恒成立 …………8分
不恒成立 …………8分又当
 时,
时, 在点
在点 处取最大值,
处取最大值,且
 ………………10分
………………10分令
 得
得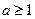
故若
 对
对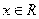 恒成立,则
恒成立,则 的取值范围是
的取值范围是  ……12分
……12分略

练习册系列答案
 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
 的方程
的方程 有一个负根,但没有正根,则实数
有一个负根,但没有正根,则实数 的取值范围是
的取值范围是  ,
, 的奇偶性;
的奇偶性; 上是减函数。
上是减函数。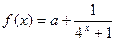 是奇函数.
是奇函数.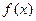 的单调性(不需要写出理由);
的单调性(不需要写出理由);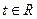 ,不等式
,不等式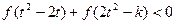 恒成立,求
恒成立,求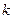 的取
的取 值范
值范 围.
围. 在区间
在区间 上无零点,则函数
上无零点,则函数 的递减区间是
的递减区间是



 在
在 为增函数,那么实数
为增函数,那么实数 的取值范围是( )
的取值范围是( )



 已知函数
已知函数 ,则
,则 的值为
的值为 的零点所在的区间是( )
的零点所在的区间是( ) )
) km,则这批货物全部运到B市最快需要________h,此时货车的速度是________km/h.
km,则这批货物全部运到B市最快需要________h,此时货车的速度是________km/h.