题目内容
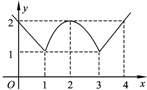 如图,函数的图象由两条射线及抛物线的一部分组成,求函数的解析式.
如图,函数的图象由两条射线及抛物线的一部分组成,求函数的解析式.分析:设左侧的射线对应解析式为y=kx+b(x≤1),利用射线过点(1,1)、(0,2)即可求得对应函数的解析式,同理可求当x≥3时,函数的解析式;最后设抛物线对应的二次函数的解析式为:y=a(x-2)2+2(1≤x≤3,a<0),求得a即可.
解答:解:设左侧的射线对应解析式为y=kx+b(x≤1).
∵点(1,1)、(0,2)在此射线上,
∴
,解得
.
∴左侧射线对应的函数的解析式为y=-x+2(x≤1),
同理,当x≥3时,函数的解析式为y=x-2(x≥3).
再设抛物线对应的二次函数的解析式为:y=a(x-2)2+2(1≤x≤3,a<0),
则∵点(1,1)在抛物线上,
∴a+2=1,a=-1.
∴抛物线对应的二次函数的解析式为:y=-x2+4x-2(1≤x≤3).
综上所述,函数的解析式为
y=
.
∵点(1,1)、(0,2)在此射线上,
∴
|
|
∴左侧射线对应的函数的解析式为y=-x+2(x≤1),
同理,当x≥3时,函数的解析式为y=x-2(x≥3).
再设抛物线对应的二次函数的解析式为:y=a(x-2)2+2(1≤x≤3,a<0),
则∵点(1,1)在抛物线上,
∴a+2=1,a=-1.
∴抛物线对应的二次函数的解析式为:y=-x2+4x-2(1≤x≤3).
综上所述,函数的解析式为
y=
|
点评:本题考查直线方程与二次函数解析式的求法,考查分析、运算及解方程组的能力,属于中档题.

练习册系列答案
相关题目

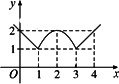
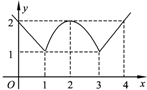 如图,函数的图象由两条射线及抛物线的一部分组成,求函数的解析式.
如图,函数的图象由两条射线及抛物线的一部分组成,求函数的解析式.