题目内容
 已知函数f(x)=2sin(x+
已知函数f(x)=2sin(x+| π |
| 6 |
(1)用五点法作出函数y=f(x)一个周期内的图象;
(2)当x∈[
| π |
| 2 |
分析:(1)利用两角和的正弦公式对解析式进行化简后,根据正弦函数图象的五个关键点列表,再由正弦函数的图象进行描点、连线;
(2)根据x的范围,观察图象并写出函数f(x)的单调区间及函数的值域.
(2)根据x的范围,观察图象并写出函数f(x)的单调区间及函数的值域.
解答:解:(1)y=2(
sinx+
cosx-cosx)=2(sinxcos
-cosxsin
)=2sin(x-
)
列表:(7分)
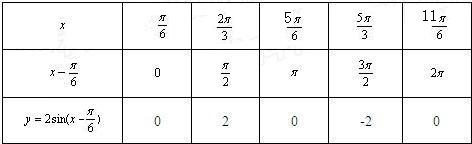
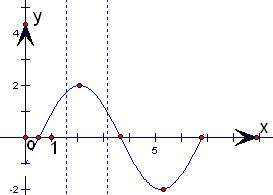
图象如图.(9分)
(2)由图象得:当x∈[
,π]时,
函数f(x)的函数的递增区间为 x∈[
,
π],
函数的递减区间为 x∈[
,π].
函数的值域[1,2].
| ||
| 2 |
| 1 |
| 2 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
列表:(7分)


图象如图.(9分)
(2)由图象得:当x∈[
| π |
| 2 |
函数f(x)的函数的递增区间为 x∈[
| π |
| 2 |
| 2 |
| 3 |
函数的递减区间为 x∈[
| 2π |
| 3 |
函数的值域[1,2].
点评:本题是关于正弦函数的性质应用的题目,需要利用公式对解析式进行化简,再由整体思想和正弦函数的性质求解,考查了整体思想和作图能力.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目