题目内容
盒子中有大小相同的球10个,其中标号为1的球3个,标号为2的球4个,标号为5的球3个.先从盒子中任取2个球(假设取到每个球的可能性相同),设取到两个球的编号之和为ξ.
(1)求随机变量ξ的分布列;
(2)求两个球编号之和大于6的概率.
(1)求随机变量ξ的分布列;
(2)求两个球编号之和大于6的概率.
(1)ξ的取值为2,3,4,6,7,10…(1分)
p(ξ=2)=
=
,
p(ξ=3)=
=
,
p(ξ=4)=
=
,
p(ξ=6)=
=
,
p(ξ=7)=
=
,
p(ξ=10)=
=
…(7分)
ξ的分布列为
…(9分)
(2)两个球编号之和大于6的概率p(ξ>6)=p(ξ=7)+p(ξ=10)=
+
=
…(13分)
p(ξ=2)=
| ||
|
| 1 |
| 15 |
p(ξ=3)=
| ||||
|
| 4 |
| 15 |
p(ξ=4)=
| ||
|
| 2 |
| 15 |
p(ξ=6)=
| ||||
|
| 1 |
| 5 |
p(ξ=7)=
| ||||
|
| 4 |
| 15 |
p(ξ=10)=
| ||
|
| 1 |
| 15 |
ξ的分布列为
| ξ | 2 | 3 | 4 | 6 | 7 | 10 | ||||||||||||
| P |
|
|
|
|
|
|
(2)两个球编号之和大于6的概率p(ξ>6)=p(ξ=7)+p(ξ=10)=
| 4 |
| 15 |
| 1 |
| 15 |
| 1 |
| 3 |

练习册系列答案
相关题目
 ,若乙先投,且两人投篮次数之和不超过4次,求
,若乙先投,且两人投篮次数之和不超过4次,求 是一个离散型随机变量,其分布列如下表,求
是一个离散型随机变量,其分布列如下表,求 值,并求
值,并求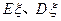 .
.





