题目内容
关于函数,给出下列命题:
①若函数f(x)是R上周期为3的偶函数,且满足f(1)=1,则f(2)-f(-4)=0;
②若函数f(x)满足f(x+1)f(x)=2 013,则f(x)是周期函数;
③若函数g(x)=
是偶函数,则f(x)=x+1;
④函数y=
的定义域为(
,+∞).
其中正确的命题是 .(写出所有正确命题的序号)
①若函数f(x)是R上周期为3的偶函数,且满足f(1)=1,则f(2)-f(-4)=0;
②若函数f(x)满足f(x+1)f(x)=2 013,则f(x)是周期函数;
③若函数g(x)=
|
④函数y=
log
|
| 3 |
| 2 |
其中正确的命题是
分析:①利用函数的周期性和奇偶性求值判断.②利用周期函数的定义证明.③利用偶函数的定义推导.④利用函数的性质求函数的定义域.
解答:解:①因为函数f(x)是R上周期为3的偶函数,所以f(2)-f(-4)=f(2-3)-f(-4+3)=f(-1)-f(1)=f(1)-f(1)=0,所以①正确.
②由f(x+1)f(x)=2 013,得f(x)≠0,所以f(x+1)f(x)=f(x+1)f(x+2)=2 013,即f(x+2)=f(x),所以函数f(x)是周期为2的周期函数,所以②正确.
③当x<0时,-x>0,所以g(-x)=-x-1,因为g(x)是偶函数,所以g(-x)=-x-1=g(x)=f(x),即x<0时,f(x)=-x-1,所以③错误.
④要使函数有意义,则有log
|2x-3|≥0,即0<|2x-3|≤1,所以0<2x-3≤1或-1≤2x-3<0,解得
<x≤2或1≤x<
,所以④错误.
故答案为:①②.
②由f(x+1)f(x)=2 013,得f(x)≠0,所以f(x+1)f(x)=f(x+1)f(x+2)=2 013,即f(x+2)=f(x),所以函数f(x)是周期为2的周期函数,所以②正确.
③当x<0时,-x>0,所以g(-x)=-x-1,因为g(x)是偶函数,所以g(-x)=-x-1=g(x)=f(x),即x<0时,f(x)=-x-1,所以③错误.
④要使函数有意义,则有log
| 1 |
| 3 |
| 3 |
| 2 |
| 3 |
| 2 |
故答案为:①②.
点评:本题考查的函数的基本性质,对应函数的奇偶性,周期性和对称性等性质要熟练掌握定义和公式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
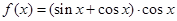 ,给出下列命题:
,给出下列命题: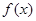 的最小正周期为
的最小正周期为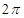 ;
;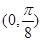 上为增函数;
上为增函数; 是函数
是函数 ,恒有
,恒有 .
.