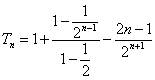题目内容
已知数列{
}的通项为
，前n项和为
，且
是
与2的等差中项；数列{
}中，b1＝1，点P（
，
）在直线x－y＋2＝0上．
（Ⅰ）求数列{
}、{
}的通项公式
、
；
（Ⅱ）设{
}的前n项和为
，试比较
与2的大小；
（Ⅲ）设若
，若
（c∈Z），求c的最小值．
答案：
解析：
解析：
（Ⅰ）解：由条件， ．∴  ，∴  ．
∴ 又 ∴ ∵ 又∵ ∴ （Ⅱ）解： ∴
∴ （Ⅲ）证明： 当 ①－②，得 ∴ 由 ∴ 满足条件 |
，∴ 
，∴ 
．
，∴ 
．
是以2为首项，公比
的等比数列． ∴ 
．
，
在直线
上，∴ 
．∴ 
．
，∴ 
是以1为首项，公差
的等差数列． 
．
． 
．
①
时，
，当
时， 
②
是递增的，∴ 
，
，又
，
的最小整数
．
练习册系列答案
互动英语系列答案
名牌学校分层周周测系列答案
黄冈海淀全程培优测试卷系列答案
相关题目