Question

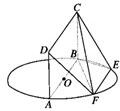如图所示，AB为圆O的直径，点E、F在圆O上，AB∥EF，矩形ABCD所在平面和圆O所在的平面互相垂直．已知AB=2，EF=1
（1）求证：平面DAF⊥平面CBF；
（2）求直线AB与平面CBF所成角的大小；
（3）当AD的长为何值时，二面角D-FE-B的大小为60°？

Answer 1

分析：（1）欲证平面DAF⊥平面CBF，先证直线与平面垂直，由题意可得：CB⊥平面ABEF，所以AF⊥CB，又在底面圆中AF⊥BF，所以AF⊥平面CBF，进一步易得平面DAF⊥平面CBF
（2）本题的设问是递进式的，第（1）问是为第（2）问作铺垫的．根据（1）的证明，有AF⊥平面CBF，所以FB为AB在平面CBF上的射影，则∠ABF为直线AB与平面CBF所成的角．
（3）二面角的度量关键在于找出它的平面角，构造平面角常用的方法就是三垂线法．由DA⊥平面ABEF可知：过点A作AM⊥EF，交EF的延长线于点M，连接DM，所以∠DMA为二面角D-FE-B的平面角，∠DMA=60°．

解答：解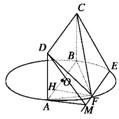：（1）证明：∵平面ABCD⊥平面ABEF，CB⊥AB，
平面ABCD∩平面ABEF=AB，
∴CB⊥平面ABEF．
∵AF?平面ABEF，∴AF⊥CB，
又∵AB为圆O的直径，∴AF⊥BF，
∴AF⊥平面CBF．
∵AF?平面DAF，∴平面DAF⊥平面CBF．
（2）根据（1）的证明，有AF⊥平面CBF，
∴FB为AB在平面CBF上的射影，
因此，∠ABF为直线AB与平面CBF所成的角．
∵AB∥EF，∴四边形ABEF为等腰梯形，
过点F作FH⊥AB，交AB于H．
AB=2，EF=1，则AH=

AB-EF

2

=

1

2

．
在Rt△AFB中，根据射影定理AF²=AH•AB，得AF=1，
sin∠ABF=

AF

AB

=

1

2

，∴∠ABF=30°，
∴直线AB与平面CBF所成角的大小为30°．
（3）过点A作AM⊥EF，交EF的延长线于点M，连接DM．
根据（1）的证明，DA⊥平面ABEF，则DM⊥EF，
∴∠DMA为二面角D-FE-B的平面角，
即∠DMA=60°．
在Rt△AFH中，∵AH=

1

2

，AF=1，
∴FH=

3

2

．
又∵四边形AMFH为矩形，∴MA=FH=

3

2

．
∵AD=MA•tan∠DMA=

3

2

•

3

=

3

2

．
因此，当AD的长为

3

2

时，二面角D-FE-B的大小为60°．

点评：本小题主要考查空间线面关系、二面角的度量等知识，考查数形结合、化归与转化的数学思想方法，以及空间想象能力、推理论证能力和运算求解能力