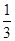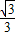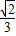题目内容
若正三棱锥的侧面都是直角三角形,则侧面与底面所成二面角的余弦值是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
分析:以正三棱锥O-ABC的顶点O为原点,OA,OB,OC为x,y,z轴建系,设侧棱长为1,分别求出侧面及底面的法向量,代入向量夹角公式,即可求出答案.
解答:解:以正三棱锥O-ABC的顶点O为原点,OA,OB,OC为x,y,z轴建系,
设侧棱长为1,
则A(1,0,0),B(0,1,0),C(0,0,1),
侧面OAB的法向量为
=(0,0,1),
底面ABC的法向量为
=(
,
,
),
∴cos<
,
>=
=
.
故选B
设侧棱长为1,
则A(1,0,0),B(0,1,0),C(0,0,1),
侧面OAB的法向量为
| OC |
底面ABC的法向量为
| n |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
∴cos<
| OC |
| n |
| ||||||||
1•
|
| ||
| 3 |
故选B
点评:本题考查的知识点是二面角的平面角及求法,向量法求二面角比较简单,但要建立恰当的坐标系.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 B.
B.
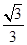 C.
C. 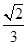 D.
D.