题目内容
已知椭圆C以F1(-1,0),F2(1,0)为焦点,且离心率e=
| ||
| 2 |
(Ⅰ)求椭圆C的方程
(Ⅱ)过M(0 ,
| 2 |
(Ⅲ)设椭圆C与x轴正半轴、y轴正半轴的交点分别为A、B,是否存在直线l1,满足(Ⅱ)中的条件且使得向量
| OP |
| OQ |
| AB |
分析:(Ⅰ)设椭圆C的半长轴长、半短轴长、半焦距长分别为a、b、c由题意可得c,根据离心率求得a,进而可得b,椭圆的方程可得.
(Ⅱ)通过点斜式设出直线l1的方程,与椭圆方程联立消去y,通过判别式大于0求得k的范围
(Ⅲ)设P(x1,y1)、Q(x2,y2),则x1、x2是(*)的二根,根据韦达定理可得求得x1+x2和y1+y2,进而可表示出
+
,根据A,B坐标求得
,若(
+
)⊥
,需(
+
)•
=0求得的k不符合(2)中的k的范围,进而可判断不存在满足题设条件的l1.
(Ⅱ)通过点斜式设出直线l1的方程,与椭圆方程联立消去y,通过判别式大于0求得k的范围
(Ⅲ)设P(x1,y1)、Q(x2,y2),则x1、x2是(*)的二根,根据韦达定理可得求得x1+x2和y1+y2,进而可表示出
| OP |
| OQ |
| AB |
| OP |
| OQ |
| AB |
| OP |
| OQ |
| AB |
解答:解:(Ⅰ)设椭圆C的半长轴长、半短轴长、半焦距长分别为a、b、c
由题设知:c=1
由e=
=
=
,得a=
,
则b=1
∴椭圆C的方程为
+y2=1
(Ⅱ)过M(0 ,
)点斜率为k的直线l1:y-
=kx
即l1:y=kx+
与椭圆C方程联立消y得(2k2+1)x2+4
x+2=0(*)
由l1与椭圆C有两个不同交点知
其△=32k2-8(2k2+1)>0得k<-
或k>
∴k的范围是(-∞,-
)∪(
,+∞).
(Ⅲ)设P(x1,y1)、Q(x2,y2),则x1、x2是(*)的二根
则x1+x2=-
,则y1+y2=k(x1+x2)+2
=
则
+
=(x1+x2,y1+y2)=(-
,
)
由题设知A(
, 0) 、B(0 , 1),∴
=(-
, 1)
若(
+
)⊥
,须(
+
)•
=
+
=0
得k=-
∉(-∞,-
)∪(
,+∞)
∴不存在满足题设条件的l1.
由题设知:c=1
由e=
| c |
| a |
| 1 |
| a |
| 1 | ||
|
| 2 |
则b=1
∴椭圆C的方程为
| x2 |
| 2 |
(Ⅱ)过M(0 ,
| 2 |
| 2 |
即l1:y=kx+
| 2 |
与椭圆C方程联立消y得(2k2+1)x2+4
| 2 |
由l1与椭圆C有两个不同交点知
其△=32k2-8(2k2+1)>0得k<-
| ||
| 2 |
| ||
| 2 |
∴k的范围是(-∞,-
| ||
| 2 |
| ||
| 2 |
(Ⅲ)设P(x1,y1)、Q(x2,y2),则x1、x2是(*)的二根
则x1+x2=-
4
| ||
| 2k2+1 |
| 2 |
2
| ||
| 2k2+1 |
则
| OP |
| OQ |
4
| ||
| 2k2+1 |
2
| ||
| 2k2+1 |
由题设知A(
| 2 |
| AB |
| 2 |
若(
| OP |
| OQ |
| AB |
| OP |
| OQ |
| AB |
| 8k |
| 2k2+1 |
2
| ||
| 2k2+1 |
得k=-
| ||
| 4 |
| ||
| 2 |
| ||
| 2 |
∴不存在满足题设条件的l1.
点评:本题主要考查了椭圆的应用.当设直线方程的时候要对斜率存不存两种情况讨论,最后还要看求得的k是否符合题意.

练习册系列答案
相关题目
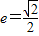
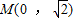 点斜率为k的直线l1与椭圆C有两个不同交点P、Q,求k的范围
点斜率为k的直线l1与椭圆C有两个不同交点P、Q,求k的范围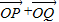 与
与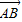 垂直?如果存在,写出l1的方程;如果不存在,请说明理由
垂直?如果存在,写出l1的方程;如果不存在,请说明理由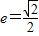
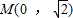 点斜率为k的直线l1与椭圆C有两个不同交点P、Q,求k的范围
点斜率为k的直线l1与椭圆C有两个不同交点P、Q,求k的范围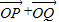 与
与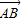 垂直?如果存在,写出l1的方程;如果不存在,请说明理由
垂直?如果存在,写出l1的方程;如果不存在,请说明理由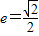
 点斜率为k的直线l1与椭圆C有两个不同交点P、Q,求k的范围
点斜率为k的直线l1与椭圆C有两个不同交点P、Q,求k的范围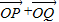 与
与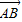 垂直?如果存在,写出l1的方程;如果不存在,请说明理由
垂直?如果存在,写出l1的方程;如果不存在,请说明理由