题目内容
求下列各组数据的方差与标准差（结果保留到小数点后一位）：
（1）1，2，3，4，5，6，7，8，9；
（2）11，12，13，14，15，16，17，18，19；
（3）10，20，30，40，50，60，70，80，90.
并分析由这些结果可得出什么一般性结论.
（1）1，2，3，4，5，6，7，8，9；
（2）11，12，13，14，15，16，17，18，19；
（3）10，20，30，40，50，60，70，80，90.
并分析由这些结果可得出什么一般性结论.
（1）s2=6.7,s=2.6；
(2)s2=6.7,s=2.6；
(3)s2=666.7,s=25.8.
所得一般性结论略.
(2)s2=6.7,s=2.6；
(3)s2=666.7,s=25.8.
所得一般性结论略.
本题考查方差、标准差的求法，并且通过三组数据的特点总结出一般规律：一组数据加上相同的数后，方差、标准差不变，都乘以相同的倍数n后，方差变为原来的n2倍，标准差变为原来的n倍.
即一组数据x1,x2,…,xn，方差为s2?，标准差为s，则x1+a,x2+a,…,xn+a方差为s2，标准差为s；nx1,nx2,…,nxn方差为n2s2，标准差为ns.
即一组数据x1,x2,…,xn，方差为s2?，标准差为s，则x1+a,x2+a,…,xn+a方差为s2，标准差为s；nx1,nx2,…,nxn方差为n2s2，标准差为ns.
练习册系列答案
相关题目
、
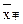分别表示甲、乙两个班的平均身高，则下列结论正确的是（ ） 
名学生，他们的数学成绩如下： 
，由此得到频率分布直方图，则这些工人中一天内生产该产品的数量在
内的频率是__________.