题目内容
若F1，F2是双曲线
与椭圆
的共同的左、右焦点，点P是两曲线的一个交点，且
为等腰三角形，则该双曲线的渐近线方程是 。
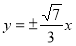
【解析】
试题分析：先利用双曲线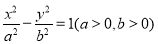
＝1（a＞0，b＞0）与椭圆
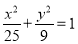＝1的共同焦点，求得a2+b2=4，再利用点P是两曲线的一个交点，且△PF1F2为等腰三角形，求得交点坐标，从而可求双曲线的标准方程，进而可求双曲线的渐近线方程.
考点：椭圆与双曲线的几何性质.
练习册系列答案
相关题目
题目内容
若F1，F2是双曲线与椭圆的共同的左、右焦点，点P是两曲线的一个交点，且为等腰三角形，则该双曲线的渐近线方程是 。
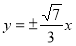
【解析】
试题分析：先利用双曲线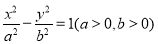＝1（a＞0，b＞0）与椭圆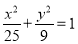＝1的共同焦点，求得a2+b2=4，再利用点P是两曲线的一个交点，且△PF1F2为等腰三角形，求得交点坐标，从而可求双曲线的标准方程，进而可求双曲线的渐近线方程.
考点：椭圆与双曲线的几何性质.
