题目内容
已知ω为正实数,函数f(x)=2sinωx在区间 上递增,那么( )
上递增,那么( )A.
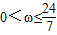
B.0<ω≤2
C.
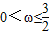
D.
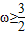
【答案】分析:先根据正弦函数在[-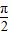 ,
,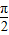 ]是增函数,再由x的范围求出wx的范围,根据单调区间得到不等式-
]是增函数,再由x的范围求出wx的范围,根据单调区间得到不等式-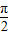 ≤-
≤-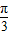 ω≤ωx≤
ω≤ωx≤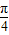 ω
ω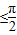 ,解出ω的范围即可得到答案.
,解出ω的范围即可得到答案.
解答:解:∵sinx在[-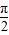 ,
,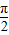 ]是增函数
]是增函数
这里-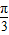 ≤x≤
≤x≤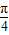
-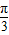 ω≤ωx≤
ω≤ωx≤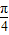 ω
ω
所以有-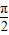 ≤-
≤-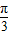 ω≤ωx≤
ω≤ωx≤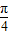 ω
ω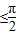
∴-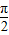 ≤
≤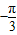 ω∴ω≤
ω∴ω≤
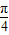 ω
ω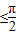 ∴ω≤2
∴ω≤2
所以0<ω≤
故选C.
点评:本题主要考查正弦函数的单调性问题.属基础题.要作对这种题型要明确理解好正弦函数的单调区间.
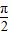 ,
,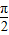 ]是增函数,再由x的范围求出wx的范围,根据单调区间得到不等式-
]是增函数,再由x的范围求出wx的范围,根据单调区间得到不等式-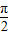 ≤-
≤-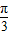 ω≤ωx≤
ω≤ωx≤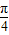 ω
ω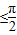 ,解出ω的范围即可得到答案.
,解出ω的范围即可得到答案.解答:解:∵sinx在[-
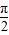 ,
,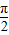 ]是增函数
]是增函数这里-
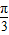 ≤x≤
≤x≤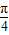
-
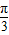 ω≤ωx≤
ω≤ωx≤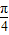 ω
ω所以有-
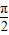 ≤-
≤-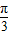 ω≤ωx≤
ω≤ωx≤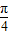 ω
ω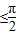
∴-
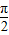 ≤
≤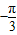 ω∴ω≤
ω∴ω≤
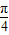 ω
ω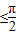 ∴ω≤2
∴ω≤2所以0<ω≤

故选C.
点评:本题主要考查正弦函数的单调性问题.属基础题.要作对这种题型要明确理解好正弦函数的单调区间.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
 、
、 为正实数,函数
为正实数,函数 在
在 上的最大值为
上的最大值为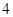 ,则
,则 在
在 上的最小值为
.
上的最小值为
. ,
, 为正实数,函数
为正实数,函数 在
在 上的最大值为
上的最大值为 ,则
,则 在
在 上的最小值为 .
上的最小值为 . (e为自然对数的底数).
(e为自然对数的底数).