题目内容
函数 的定义域为集合A,函数
的定义域为集合A,函数 的定义域为集合B.
的定义域为集合B.
(1)求A;
(2)若B A,求实数
A,求实数 的取值范围。
的取值范围。
 的定义域为集合A,函数
的定义域为集合A,函数 的定义域为集合B.
的定义域为集合B.(1)求A;
(2)若B
 A,求实数
A,求实数 的取值范围。
的取值范围。(1)A:x<-1或x≥1;(2)a>1或a≤-2或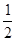 ≤a<1;
≤a<1;
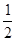 ≤a<1;
≤a<1; 试题分析: (1)首先利用分式不等式得到集合A。
(2)同时利用对数真数大于零得到集合B,然后根据集合A,B的包含关系,借助于数轴法得到参数a的范围。
(1)A:x<-1或x≥1; --------------------------------3分
(2)B:(x-a-1)(x-2a)<0
∵φ≠B
 A,∴①
A,∴① 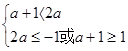 ∴a>1 ------------------------6分
∴a>1 ------------------------6分或②
 ∴a≤-2或
∴a≤-2或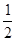 ≤a<1; ---------------------------8分
≤a<1; ---------------------------8分∴a>1或a≤-2或
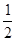 ≤a<1; -------------10分
≤a<1; -------------10分点评:解决该试题的关键是理解分式不等式的求解,以及对数函数定义域的求解,利用结合的包含关系,结合数轴法得到结论。

练习册系列答案
相关题目
 ,则
,则 ( )
( )



 ,集合
,集合 ,集合
,集合 ,则
,则




 ,且
,且 ,则集合
,则集合 可能是( )
可能是( )



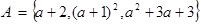 ,若
,若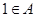 ,则实数
,则实数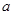 的值为
的值为 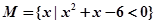 ,
,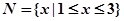 ,则
,则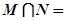 ( )
( )

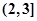

 ,且
,且 ,则实数
,则实数 的取值范围是 .
的取值范围是 . ,集合
,集合 ,
,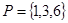 ,则集合
,则集合 是( )
是( )



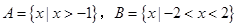 ,则
,则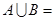 ( )
( )


