Question

由直线y=x-2，曲线y=

x

以及x轴所围成的图形的面积为

10

3

．

Answer 1

分析：先求出两曲线的交点坐标，再由面积与积分的关系将面积用积分表示出来，由公式求出积分，即可得到面积值

解答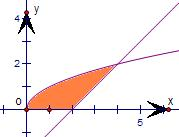：解：联立方程

y= x y=x-2

得到两曲线的交点（4，2），
故由直线y=x-2，曲线y=

x

以及x轴所围成的图形的面积为：
∫₀²

x

dx+∫₂⁴（

x

-x+2）dx=

2

3

x

3

2

|

2 0

+(

2

3

x

3

2

+2x-

1

2

x2)

|

4 2

=

10

3

．
故答案为：

10

3

．

点评：本题考查定积分在求面积中的应用，解答本题关键是根据题设中的条件建立起面积的积分表达式，再根据相关的公式求出积分的值，用定积分求面积是其重要运用，掌握住一些常用函数的导数的求法是解题的知识保证