题目内容
由曲线y=
和直线y=x-4,x=1,x=2围成的曲边梯形的面积是
| 1 | x |
ln2+1
ln2+1
.分析:曲线y=
与直线y=x-4,x=2,x=1所围成的图形面积可用定积分计算,先求出图形横坐标范围,再代入定积分的公式求出结果即可.
| 1 |
| x |
解答:解:联立两条直线的方程
,得
和
∴曲线y=
与直线y=x-4,x=2,x=1所围成的图形面积为
(
-x+4)dx=(-x2+lnx+4x)|12=ln2+1
故答案为:ln2+1
|
|
|
∴曲线y=
| 1 |
| x |
| ∫ | 1 2 |
| 1 |
| x |
故答案为:ln2+1
点评:本题考查利用定积分求封闭图形的面积,解题的关键是利用方程联立做出两个函数的交点坐标,不停地交点的坐标在解题中用不到,本题是一个基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
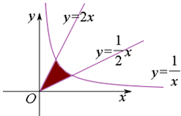
 如图,在第一象限由直线y=2x,
如图,在第一象限由直线y=2x,