题目内容
(1)选修4-2:矩阵与变换如图,矩形OABC的顶点O(0,0)、A(-2,0)、B(-2,-1)、C(0,-1).将矩形OABC绕坐标原点O旋转得到矩形OA1B1C1;再将矩形OA1B1C1沿x轴正方向作切变变换,得到平行四边形OA1B2C2,且点C2的坐标为(
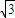 ,1).求将矩形OABC变为平行四边形OA1B2C2的线性变换对应的矩阵.
,1).求将矩形OABC变为平行四边形OA1B2C2的线性变换对应的矩阵.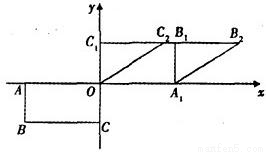
【答案】分析:先根据矩形OA1B1C1是矩阵OABC绕原点O旋转180°得到的求出A1,B1,C1的坐标,再根据矩形OA1B1C1沿x轴正方向作切变变换得到平行四边形OA1B2C2,且点C2的坐标为(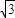 ,1)求出点B2的坐标,最后利用待定系数法建立等式,解之即可.
,1)求出点B2的坐标,最后利用待定系数法建立等式,解之即可.
解答:解:因为矩形OA1B1C1是矩阵OABC绕原点O旋转180°得到的,
所以A1(2,0),B1(2,1),C1(0,1)
又矩形OA1B1C1沿x轴正方向作切变变换得到平行四边形OA1B2C2,且点C2的坐标为(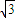 ,1)
,1)
所以点B2的坐标为(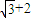 ,1)
,1)
设将矩形OABC变为平行四边形OA1B2C2的线性变换对于的矩阵为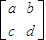
则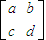
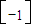 =
=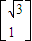 ,
,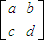
 =
=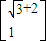
所以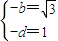 ,
,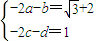
得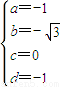 ,因此所求矩阵为
,因此所求矩阵为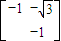
点评:本题主要考查矩阵与变换等基础知识,考查运算求解能力,考查数形结合思想、分类与整合思想,属于基础题.
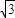 ,1)求出点B2的坐标,最后利用待定系数法建立等式,解之即可.
,1)求出点B2的坐标,最后利用待定系数法建立等式,解之即可.解答:解:因为矩形OA1B1C1是矩阵OABC绕原点O旋转180°得到的,
所以A1(2,0),B1(2,1),C1(0,1)
又矩形OA1B1C1沿x轴正方向作切变变换得到平行四边形OA1B2C2,且点C2的坐标为(
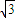 ,1)
,1)所以点B2的坐标为(
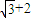 ,1)
,1)设将矩形OABC变为平行四边形OA1B2C2的线性变换对于的矩阵为
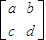
则
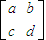
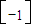 =
=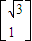 ,
,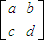
 =
=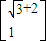
所以
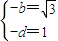 ,
,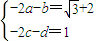
得
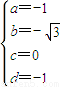 ,因此所求矩阵为
,因此所求矩阵为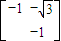
点评:本题主要考查矩阵与变换等基础知识,考查运算求解能力,考查数形结合思想、分类与整合思想,属于基础题.

练习册系列答案
相关题目
 如图,△ABC是⊙O的内接三角形,PA是⊙O的切线,PB交AC于点E,交⊙O于点D,若PE=PA,
如图,△ABC是⊙O的内接三角形,PA是⊙O的切线,PB交AC于点E,交⊙O于点D,若PE=PA, ,PD=1,BD=8,求线段BC的长.
,PD=1,BD=8,求线段BC的长. ,矩阵阵
,矩阵阵 ,
, ,求在矩阵
,求在矩阵 作用下变换所得到的图形的面积.
作用下变换所得到的图形的面积. (
( 为参数,
为参数, 为常数且
为常数且 )被以原点为极点,
)被以原点为极点, 轴的正半轴为极轴,方程为
轴的正半轴为极轴,方程为 的曲线所截,求截得的弦长.
的曲线所截,求截得的弦长. ,求证:
,求证: .
.