题目内容
1.棱长为1的正方体ABCD-A1B1C1D1中,E、F分别是BC、A1D1的中点,求AD和平面B1EDF所成角的正弦值.分析 首先以D为原点,直线DA,DC,DD1分别为x,y,z轴建立空间直角坐标系,然后可确定一些点的坐标,设平面B1EDF的法向量为$\overrightarrow{n}$,而根据$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{DE}=0}\\{\overrightarrow{n}•\overrightarrow{DF}=0}\end{array}\right.$即可求出法向量$\overrightarrow{n}$.设直线AD和平面B1EDF所成角为θ,根据sinθ=$|cos<\overrightarrow{n},\overrightarrow{DA}>|$即可求出sinθ.
解答 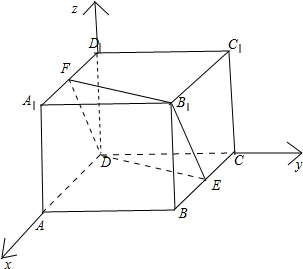 解:如图,分别以边DA,DC,DD1所在直线为x,y,z轴建立空间直角坐标系,设正方体的边长为2,则:
解:如图,分别以边DA,DC,DD1所在直线为x,y,z轴建立空间直角坐标系,设正方体的边长为2,则:
D(0,0,0),E(1,2,0),F(1,0,2),A(2,0,0);
∴$\overrightarrow{DE}=(1,2,0),\overrightarrow{DF}=(1,0,2)$,$\overrightarrow{DA}=(2,0,0)$;
设平面B1EDF的法向量为$\overrightarrow{n}=(x,y,z)$,则:$\overrightarrow{n}⊥\overrightarrow{DE},\overrightarrow{n}⊥\overrightarrow{DF}$;
∴$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{DE}=0}\\{\overrightarrow{n}•\overrightarrow{DF}=0}\end{array}\right.$;
∴$\left\{\begin{array}{l}{x+2y=0}\\{x+2z=0}\end{array}\right.$;
∴$\left\{\begin{array}{l}{y=-\frac{1}{2}x}\\{z=-\frac{1}{2}x}\end{array}\right.$,取x=1,∴$\overrightarrow{n}=(1,-\frac{1}{2},-\frac{1}{2})$;
若设直线AD和平面B1EDF所成角为θ,则:
sinθ=|cos$<\overrightarrow{n},\overrightarrow{DA}>$|=$\frac{|\overrightarrow{n}•\overrightarrow{DA}|}{|\overrightarrow{n}||\overrightarrow{DA}|}=\frac{2}{2•\sqrt{\frac{3}{2}}}=\frac{\sqrt{6}}{3}$;
∴直线AD和平面B1EDF所成角的正弦值为$\frac{\sqrt{6}}{3}$.
点评 考查建立空间直角坐标系,利用空间向量求线面角的方法,能确定空间点的坐标,以及平面法向量的概念,向量夹角余弦的坐标公式,弄清直线和法向量所成角与直线和平面所成角的关系.

| 日期 | 3月1日 | 3月2日 | 3月3日 | 3月4日 | 3月5日 |
| 温差x (度) | 10 | 11 | 13 | 12 | 9 |
| 发芽数y(颗) | 15 | 16 | 17 | 14 | 13 |
(1)请根据3月1日至3月5日的数据,求出y关于x的线性回归方程.据气象预报3月6日的昼夜温差为11℃,请预测3月6日浸泡的30颗种子的发芽数.(结果保留整数)
(2)从3月1日至3月5日中任选两天,记种子发芽数超过15颗的天数为X,求X的概率分布列,并求其数学期望和方差.
 如图,△ABC内接于直径为BC的圆O,过点A作圆O的切线交CB的延长线于点P,∠BAC的平分线分别交BC和圆O于点D、E,若PA=2PB=10.
如图,△ABC内接于直径为BC的圆O,过点A作圆O的切线交CB的延长线于点P,∠BAC的平分线分别交BC和圆O于点D、E,若PA=2PB=10.(1)求证:AC=2AB;
(2)求AD•DE的值.
| A. | [-2,-$\frac{1}{3}$] | B. | [-2,+∞) | C. | (-∞,-$\frac{1}{3}$] | D. | (-∞,-2] |
 如图,四棱锥P-ABCD中,PA⊥平面ABCD,PA=$\sqrt{6}$,四边形ABCD是边长为2的菱形,∠ABC=60°,M,N分别为BC和PB的中点.
如图,四棱锥P-ABCD中,PA⊥平面ABCD,PA=$\sqrt{6}$,四边形ABCD是边长为2的菱形,∠ABC=60°,M,N分别为BC和PB的中点. 为了解某地高中生身高情况,研究小组在该地高中生中随机抽取30名高中生的身高编成如图所示的茎叶图(单位:cm);若身高在175cm以上(包括175cm)定义为“高个子”,身高在175以下(不包括175cm)定义为“非高个子”.
为了解某地高中生身高情况,研究小组在该地高中生中随机抽取30名高中生的身高编成如图所示的茎叶图(单位:cm);若身高在175cm以上(包括175cm)定义为“高个子”,身高在175以下(不包括175cm)定义为“非高个子”.