题目内容
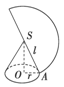
如果圆锥的侧面展开图是半圆，那么这个圆锥的母线与轴线所成的角为
．
| π |
| 6 |
| π |
| 6 |
分析：由题意，半圆的弧长与圆锥底面圆的周长是相等的，且圆锥的母线与轴线所成的角的正弦值是圆锥底面圆的半径r与圆锥母线长的比，即圆锥底面圆的半径r与半圆半径R的比，由此易求得角
解答：解：圆锥的侧面展开图是半圆，那么这个圆锥的母线与轴线所成的角的正弦值是圆锥底面圆的半径r与圆锥母线长的比，即圆锥底面圆的半径r与半圆半径R的比
由题意πR=2πr，即有
=
∴这个圆锥的母线与轴线所成的角为
故答案为
由题意πR=2πr，即有
| r |
| R |
| 1 |
| 2 |
∴这个圆锥的母线与轴线所成的角为
| π |
| 6 |
故答案为
| π |
| 6 |
点评：本题考点是旋转体，考查了图形折叠问题中的变与不变，解题的关键是有着较强的空间感知能力，能想像出圆锥的母线与轴线所成的角的几何位置特征，本题考察了空间想像能力及判断推理的能力
练习册系列答案
相关题目
