题目内容
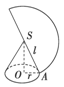
如果圆锥的侧面展开图是半圆，那么这个圆锥的轴截面中两条母线的夹角是
60°
60°
．分析：由侧面展开图的圆心角计算公式，结合题意可得圆锥的母线长等于底面半径的2倍，由此在圆锥的高与母线构成的直角三角形中，利用三角函数的定义加以计算，即可算出圆锥的轴截面中两条母线的夹角大小．
解答：解：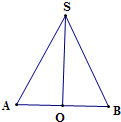
设轴截面为如图等腰△SAB，O是AB的中点，即底面圆的圆心，圆锥的底面圆半径为r，母线为l，
∵圆锥的侧面展开图是半圆，
∴侧面展开图的圆心角为180°，即
×360°=180°，可得l=2r．
Rt△SOA中，sin∠ASO=
=
=
，可得∠ASO=30°，
因此∠ASB=2∠ASO=60°，即轴截面中两条母线的夹角是60°．
故答案为：60°
设轴截面为如图等腰△SAB，O是AB的中点，即底面圆的圆心，圆锥的底面圆半径为r，母线为l，∵圆锥的侧面展开图是半圆，
∴侧面展开图的圆心角为180°，即
| r |
| l |
Rt△SOA中，sin∠ASO=
| AO |
| SA |
| r |
| l |
| 1 |
| 2 |
因此∠ASB=2∠ASO=60°，即轴截面中两条母线的夹角是60°．
故答案为：60°
点评：本题给出圆锥的侧面展开图的形状，求轴截面中两条母线的夹角．着重考查了圆锥的性质、圆锥的侧面展开图和解直角三角形等知识，属于基础题．
练习册系列答案
相关题目
