题目内容
已知矩形ABCD中AB=4,BC=3,将其沿对角线AC折起,形成四面体ABCD,则以下命题正确的是:
①四面体ABCD体积最大值为
;
②四面体ABCD中,AB⊥CD;
③四面体ABCD的侧视图可能是个等腰直角三角形;
④四面体ABCD的外接球表面积是25π.
①③④
①③④
(写出所有正确命题的序号)①四面体ABCD体积最大值为
| 24 | 5 |
②四面体ABCD中,AB⊥CD;
③四面体ABCD的侧视图可能是个等腰直角三角形;
④四面体ABCD的外接球表面积是25π.
分析:①四面体ABCD体积最大值时为两个面互相垂直,求出体积即可判断正误;
②四面体ABCD中,AB⊥CD;当两个面互相垂直时才能满足;
③四面体ABCD的侧视图可能是个等腰直角三角形;当两个面互相垂直时就能满足;
④求出四面体ABCD的外接球表面积即可判断正误.
②四面体ABCD中,AB⊥CD;当两个面互相垂直时才能满足;
③四面体ABCD的侧视图可能是个等腰直角三角形;当两个面互相垂直时就能满足;
④求出四面体ABCD的外接球表面积即可判断正误.
解答:解:①四面体ABCD体积最大值为两个面互相垂直,它的体积为
;所以①正确;
②四面体ABCD中,AB⊥CD;当两个面互相垂直时才能满足;所以不正确;
③四面体ABCD的侧视图可能是个等腰直角三角形;当两个面互相垂直时就能满足;正确;
④通过就是四面体ABCD的外接球表面积是25π,所以正确.
故答案为:①③④
| 24 |
| 5 |
②四面体ABCD中,AB⊥CD;当两个面互相垂直时才能满足;所以不正确;
③四面体ABCD的侧视图可能是个等腰直角三角形;当两个面互相垂直时就能满足;正确;
④通过就是四面体ABCD的外接球表面积是25π,所以正确.
故答案为:①③④
点评:本题是基础题,考查四面体ABCD的外接球的表面积,三视图,垂直关系,三棱锥的体积,是综合题,每一个选项都必须认真验证,或找出反例,是常考题.

练习册系列答案
相关题目
 已知矩形ABCD中,
已知矩形ABCD中,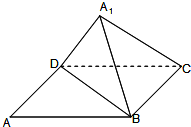 如图,已知矩形ABCD中,AB=10,BC=6,将矩形沿对角线BD把△ABD折起,使A移到A1点,且A1在平面BCD上的射影O恰好在CD上.
如图,已知矩形ABCD中,AB=10,BC=6,将矩形沿对角线BD把△ABD折起,使A移到A1点,且A1在平面BCD上的射影O恰好在CD上.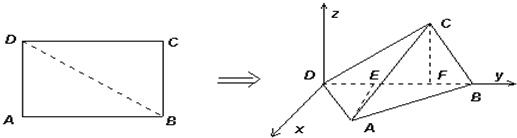
 (2013•温州二模)已知矩形ABCD中,AB=2,AD=5.E,F分别在AD,BC上.且AE=1,BF=3,沿EF将四边形AEFB折成四边形A′EFB′,使点B′在平面CDEF 上的射影H在直线DE上.
(2013•温州二模)已知矩形ABCD中,AB=2,AD=5.E,F分别在AD,BC上.且AE=1,BF=3,沿EF将四边形AEFB折成四边形A′EFB′,使点B′在平面CDEF 上的射影H在直线DE上.