题目内容
圆锥SO的底面半径为
,母线长2,A,B是底面圆周上两动点,过S,A,B作圆锥的截面,当△SAB的面积最大时,截面SAB与底面圆O所成的(不大于
的)二面角等于( )
| 3 |
| π |
| 2 |
分析:利用圆锥的轴截面和截面的性质、直角三角形的性质、勾股定理、二面角的定义、三垂线定理即可得出.
解答:解:如图所示,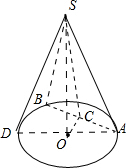 在轴截面△SAD,Rt△SAO中,sin∠ASO=
在轴截面△SAD,Rt△SAO中,sin∠ASO=
=
,∴∠ASO=60°,∴∠ASD=120°.
因此当△SAB的面积最大时,∠ASB可取得90°.于是AB=
SA=2
.
取AB的中点C,连接OC,SC.
则OC⊥AB,∵SO⊥底面ABD,∴AB⊥SC,∴∠SCO即为截面SAB与底面圆O所成的(不大于
的)二面角.
在Rt△OCA中,OC=
=
=1.
在Rt△SOA中,OS=
=1.
在Rt△SOC中,tan∠SCO=
=1,∴∠SCO=
.
故选B.
 在轴截面△SAD,Rt△SAO中,sin∠ASO=
在轴截面△SAD,Rt△SAO中,sin∠ASO=| OA |
| SA |
| ||
| 2 |
因此当△SAB的面积最大时,∠ASB可取得90°.于是AB=
| 2 |
| 2 |
取AB的中点C,连接OC,SC.
则OC⊥AB,∵SO⊥底面ABD,∴AB⊥SC,∴∠SCO即为截面SAB与底面圆O所成的(不大于
| π |
| 2 |
在Rt△OCA中,OC=
| OA2-AC2 |
(
|
在Rt△SOA中,OS=
| SA2-OA2 |
在Rt△SOC中,tan∠SCO=
| SO |
| OC |
| π |
| 4 |
故选B.
点评:熟练掌握圆锥的轴截面和截面的性质、直角三角形的性质、勾股定理、二面角的定义、三垂线定理等是解题的关键.

练习册系列答案
相关题目
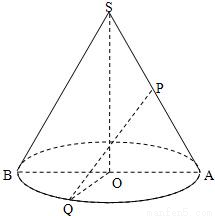
 如图,已知圆锥的底面半径为r=10,点Q为半圆弧
如图,已知圆锥的底面半径为r=10,点Q为半圆弧
 如图,已知圆锥的底面半径为r=10,点Q为半圆弧
如图,已知圆锥的底面半径为r=10,点Q为半圆弧 的中点,点P为母线SA的中点.若PQ与SO所成角为
的中点,点P为母线SA的中点.若PQ与SO所成角为 ,求此圆锥的全面积与体积.
,求此圆锥的全面积与体积. 的中点,点P为母线SA的中点.若PQ与SO所成角为
的中点,点P为母线SA的中点.若PQ与SO所成角为 ,求此圆锥的全面积与体积.
,求此圆锥的全面积与体积.
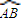 的中点,点P为母线SA的中点.若PQ与SO所成角为
的中点,点P为母线SA的中点.若PQ与SO所成角为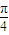 ,求此圆锥的全面积与体积.
,求此圆锥的全面积与体积.