题目内容
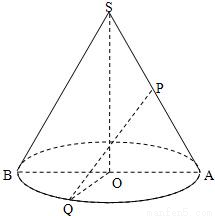
 如图,已知圆锥的底面半径为r=10,点Q为半圆弧
如图,已知圆锥的底面半径为r=10,点Q为半圆弧 的中点,点P为母线SA的中点.若PQ与SO所成角为
的中点,点P为母线SA的中点.若PQ与SO所成角为 ,求此圆锥的全面积与体积.
,求此圆锥的全面积与体积.
解:取OA的中点H,连接PH,QH,
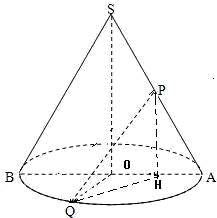
则PH∥SO且PH= SO,
SO,
∵PH⊥平面AQB,且∠QPH= ,在直角三角形△QOH中,QH=5
,在直角三角形△QOH中,QH=5 ,
,
在直角三角形△PHQ中,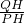 =tan
=tan =1,则PH=5
=1,则PH=5 ,即SO=10
,即SO=10 ,
,
在直角三角形△SOA中,SA= =10
=10 ,
,
∴圆锥的全面积S=πr2+πr•SA=100π+10 π,
π,
圆锥的体积V= πr2•SO=
πr2•SO= π×100×10
π×100×10 =
=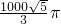 ,
,
分析:由题意和几何体的特征,取OA的中点H,连接PH,QH,利用线面垂直和勾股定理求出母线长和圆锥的高.再代入全面积公式和体积公式求值.
点评:本题考查了求圆锥的全面积和体积,主要根据几何体的结构特征、直角三角形、题中的条件,求出锥体的母线长和高,进而求出对应的值,考查了分析和解决问题的能力.

则PH∥SO且PH=
 SO,
SO,∵PH⊥平面AQB,且∠QPH=
 ,在直角三角形△QOH中,QH=5
,在直角三角形△QOH中,QH=5 ,
,在直角三角形△PHQ中,
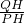 =tan
=tan =1,则PH=5
=1,则PH=5 ,即SO=10
,即SO=10 ,
,在直角三角形△SOA中,SA=
 =10
=10 ,
,∴圆锥的全面积S=πr2+πr•SA=100π+10
 π,
π,圆锥的体积V=
 πr2•SO=
πr2•SO= π×100×10
π×100×10 =
=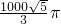 ,
,分析:由题意和几何体的特征,取OA的中点H,连接PH,QH,利用线面垂直和勾股定理求出母线长和圆锥的高.再代入全面积公式和体积公式求值.
点评:本题考查了求圆锥的全面积和体积,主要根据几何体的结构特征、直角三角形、题中的条件,求出锥体的母线长和高,进而求出对应的值,考查了分析和解决问题的能力.

练习册系列答案
相关题目
 如图,已知圆锥的底面半径为r=10,点Q为半圆弧
如图,已知圆锥的底面半径为r=10,点Q为半圆弧
 如图,已知圆锥的底面直径和母线长均为4,过OA上一点P作平面α,当OB∥α时平面a截圆锥所得的截口曲线为抛物线,设抛物线的焦点为F,若OP=1,则|PF|长为( )
如图,已知圆锥的底面直径和母线长均为4,过OA上一点P作平面α,当OB∥α时平面a截圆锥所得的截口曲线为抛物线,设抛物线的焦点为F,若OP=1,则|PF|长为( ) 的中点,点P为母线SA的中点.若PQ与SO所成角为
的中点,点P为母线SA的中点.若PQ与SO所成角为 ,求此圆锥的全面积与体积.
,求此圆锥的全面积与体积.
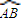 的中点,点P为母线SA的中点.若PQ与SO所成角为
的中点,点P为母线SA的中点.若PQ与SO所成角为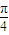 ,求此圆锥的全面积与体积.
,求此圆锥的全面积与体积.