题目内容
已知函数f(x),如果存在给定的实数对(a,b),使得f(a+x)•f(a-x)=b恒成立,则称f(x)为“S-函数”.(1)判断函数f1(x)=x,f2(x)=3x是否是“S-函数”;
(2)若f3(x)=tanx是一个“S-函数”,求出所有满足条件的有序实数对(a,b);
(3)若定义域为R的函数f(x)是“S-函数”,且存在满足条件的有序实数对(0,1)和(1,4),当x∈[0,1]时,f(x)的值域为[1,2],求当x∈[-2012,2012]时函数f(x)的值域.
【答案】分析:(1)假设是S-函数,列出方程恒成立,通过判断方程的解的个数判断出f1(x)不是,对于f2(x)对于列出方程恒成立.
(2)据题中的定义,列出方程恒成立,通过两角和差的正切公式展开整理,令含未知数的系数为0,求出a,b.
(3)利用题中的新定义,列出两个等式恒成立;将x用2+x代替,两等式结合得到函数值的递推关系;用不完全归纳的方法求出值域.
解答:解:(1)若f1(x)=x是“S-函数”,则存在常数(a,b),使得(a+x)(a-x)=b.
即x2=a2-b时,对x∈R恒成立.而x2=a2-b最多有两个解,矛盾,
因此f1(x)=x不是“S-函数”.(3分)
若f2(x)=3x是“S-函数”,则存在常数a,b使得3a+x•3a-x=32a,
即存在常数对(a,32a)满足.
因此f2(x)=3x是“S-函数”(6分)
(2)f3(x)=tanx是一个“S-函数”,设有序实数对(a,b)满足:
则tan(a-x)tan(a+x)=b恒成立.
当a=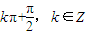 时,tan(a-x)tan(a+x)=-cot2(x),不是常数.(7分)
时,tan(a-x)tan(a+x)=-cot2(x),不是常数.(7分)
因此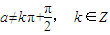 ,
,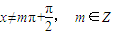 ,
,
则有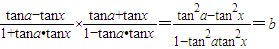 .
.
即(b•tan2a-1)tan2x+(tan2a-b)=0恒成立.(9分)
即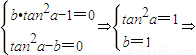
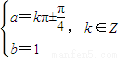 ,
,
当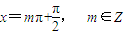 ,
,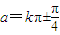 时,tan(a-x)tan(a+x)=cot2(a)=1.
时,tan(a-x)tan(a+x)=cot2(a)=1.
因此满足f3(x)=tanx是一个“S-函数”的常数(a,b)=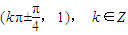 .(12分)
.(12分)
(3)函数f(x)是“S-函数”,且存在满足条件的有序实数对(0,1)和(1,4),
于是f(x)•f(-x)=1,f(1+x)•f(1-x)=4,
即f(1+x)•f(1-x)=4?f(x)f(2-x)=4,x∈[1,2]时,2-x∈[0,1],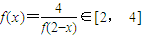 ,
,
∴x∈[0,2]时,f(x)∈[1,4].(14分)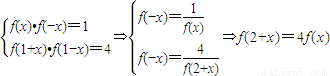 .(16分)
.(16分)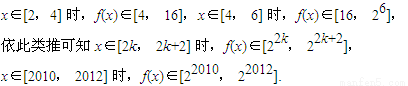
因此x∈[0,2012]时,f(x)∈[1,22012],(17分)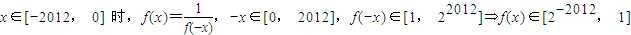 .
.
综上可知当x∈[-2012,2012]时函数f(x)的值域为[2-2012,22012].(18分)
点评:本题考查理解题中的新定义、判断函数是否具有特殊函数的条件、利用新定义得到恒等式、通过仿写的方法得到函数的递推关系、考查利用归纳的方法得结论.
(2)据题中的定义,列出方程恒成立,通过两角和差的正切公式展开整理,令含未知数的系数为0,求出a,b.
(3)利用题中的新定义,列出两个等式恒成立;将x用2+x代替,两等式结合得到函数值的递推关系;用不完全归纳的方法求出值域.
解答:解:(1)若f1(x)=x是“S-函数”,则存在常数(a,b),使得(a+x)(a-x)=b.
即x2=a2-b时,对x∈R恒成立.而x2=a2-b最多有两个解,矛盾,
因此f1(x)=x不是“S-函数”.(3分)
若f2(x)=3x是“S-函数”,则存在常数a,b使得3a+x•3a-x=32a,
即存在常数对(a,32a)满足.
因此f2(x)=3x是“S-函数”(6分)
(2)f3(x)=tanx是一个“S-函数”,设有序实数对(a,b)满足:
则tan(a-x)tan(a+x)=b恒成立.
当a=
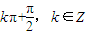 时,tan(a-x)tan(a+x)=-cot2(x),不是常数.(7分)
时,tan(a-x)tan(a+x)=-cot2(x),不是常数.(7分)因此
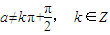 ,
,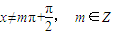 ,
,则有
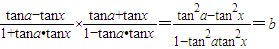 .
.即(b•tan2a-1)tan2x+(tan2a-b)=0恒成立.(9分)
即
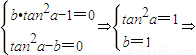
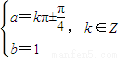 ,
,当
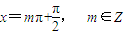 ,
,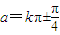 时,tan(a-x)tan(a+x)=cot2(a)=1.
时,tan(a-x)tan(a+x)=cot2(a)=1.因此满足f3(x)=tanx是一个“S-函数”的常数(a,b)=
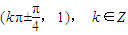 .(12分)
.(12分)(3)函数f(x)是“S-函数”,且存在满足条件的有序实数对(0,1)和(1,4),
于是f(x)•f(-x)=1,f(1+x)•f(1-x)=4,
即f(1+x)•f(1-x)=4?f(x)f(2-x)=4,x∈[1,2]时,2-x∈[0,1],
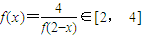 ,
,∴x∈[0,2]时,f(x)∈[1,4].(14分)
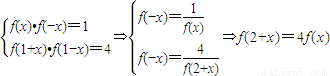 .(16分)
.(16分)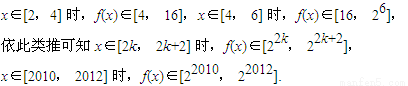
因此x∈[0,2012]时,f(x)∈[1,22012],(17分)
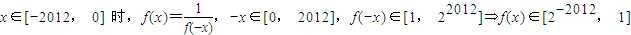 .
.综上可知当x∈[-2012,2012]时函数f(x)的值域为[2-2012,22012].(18分)
点评:本题考查理解题中的新定义、判断函数是否具有特殊函数的条件、利用新定义得到恒等式、通过仿写的方法得到函数的递推关系、考查利用归纳的方法得结论.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
 6、已知函数f(x)的导函数f′(x)=ax2+bx+c的图象如图,则f(x)的图象可能是( )
6、已知函数f(x)的导函数f′(x)=ax2+bx+c的图象如图,则f(x)的图象可能是( ) 已知函数f(x)=ax+b(a>0且a≠1)的图象如图所示,则a,b的值分别是( )
已知函数f(x)=ax+b(a>0且a≠1)的图象如图所示,则a,b的值分别是( ) 已知函数f(x)的定义域为[-1,5],部分对应值如下表.
已知函数f(x)的定义域为[-1,5],部分对应值如下表. (理)已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
(理)已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|< 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0)的部分图象如图所示,则y=f(x)的图象可由函数g(x)=sinx的图象(纵坐标不变)( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0)的部分图象如图所示,则y=f(x)的图象可由函数g(x)=sinx的图象(纵坐标不变)( )