Question

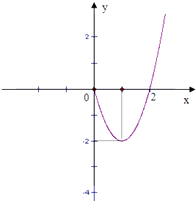
【题目】已知抛物线，直线交于两点， 是的中点，过作轴的垂线交于点.

（1）证明：抛物线在点处的切线与平行；

（2）是否存在实数，使以为直径的圆经过点？若存在，求出的值；若不存在，请说明理由.

Answer 1

【答案】(1)见解析;(2) 存在实数使以为直径的圆经过点.

【解析】【试题分析】（1）先运用直线与抛物线的位置关系求出切点坐标，再求导运用导数的几何意义分析推证；（2）依据题设条件借助（1）的结论分析探求：

（1）证明：设， ，把代入得.

所以， ，所以.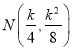

因为，所以抛物线在点处的切线斜率为，故该切线与平行.

（2）假设存在实数，使以为直径的圆经过点，则.

由（1）知 ，又因为垂直于轴，

所以，

而 .

所以，解得.

所以，存在实数使以为直径的圆经过点.